题目内容
 如图,在△ABC中,∠B=22.5°,∠C=60°,线段AB的垂直平分线FD分别交BC,AB于点D,F,AE⊥BC,垂足为点E,EC=2
如图,在△ABC中,∠B=22.5°,∠C=60°,线段AB的垂直平分线FD分别交BC,AB于点D,F,AE⊥BC,垂足为点E,EC=2| 3 |
考点:勾股定理,线段垂直平分线的性质
专题:
分析:首先作出辅助线连接AD,再在Rt△AEC中,利用勾股定理得到AE的长,利用线段垂直平分线的性质和勾股定理得到BD的长.
解答: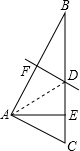 解:连接AD.
解:连接AD.
在Rt△AEC中,∠EAC=90°-60°=30°.
∴AC=2EC=4
,
∴AE=
=6.
∵FD垂直平分AB,∠B=22.5°,
∴∠ADC=45°.
∴AE=ED=6.
∴Rt△AED中,AD=
=6
.
∵FD垂直平分AB,
∴BD=AD.
∴BD=6
.
 解:连接AD.
解:连接AD.在Rt△AEC中,∠EAC=90°-60°=30°.
∴AC=2EC=4
| 3 |
∴AE=
(4
|
∵FD垂直平分AB,∠B=22.5°,
∴∠ADC=45°.
∴AE=ED=6.
∴Rt△AED中,AD=
| 62+62 |
| 2 |
∵FD垂直平分AB,
∴BD=AD.
∴BD=6
| 2 |
点评:考查勾股定理,的线段垂直平分线的性质(垂直平分线上任意一点,和线段两端点的距离相等)有关知识.本题关键是作出辅助线连接AD.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
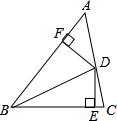 如图,∠ABC=60°,点D在AC上,BD=16,DE⊥BC,DF⊥AB,且DE=DF,求:
如图,∠ABC=60°,点D在AC上,BD=16,DE⊥BC,DF⊥AB,且DE=DF,求: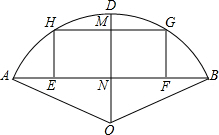 已知,如图,以O为圆心,OA为半径画弧,∠AOB=120°,弓形高ND=4厘米,矩形EFGH的两顶点E,F在弦AB上,H,G在
已知,如图,以O为圆心,OA为半径画弧,∠AOB=120°,弓形高ND=4厘米,矩形EFGH的两顶点E,F在弦AB上,H,G在
 如图,在方格纸上建立平面直角坐标系,每个小正方形的边长为1.
如图,在方格纸上建立平面直角坐标系,每个小正方形的边长为1.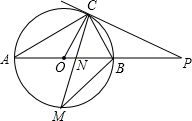 如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,连AC、OC,若AC=PC,∠P=30°.
如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,连AC、OC,若AC=PC,∠P=30°. 如图,在△ABC中,AB的垂直平分线MN交AB于点D,交AC于点E,且AC=15cm,△BCD的周长等于25cm.
如图,在△ABC中,AB的垂直平分线MN交AB于点D,交AC于点E,且AC=15cm,△BCD的周长等于25cm.