题目内容
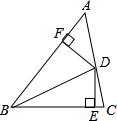 如图,∠ABC=60°,点D在AC上,BD=16,DE⊥BC,DF⊥AB,且DE=DF,求:
如图,∠ABC=60°,点D在AC上,BD=16,DE⊥BC,DF⊥AB,且DE=DF,求:(1)∠CBD的度数;
(2)DF的长度.
考点:角平分线的性质,含30度角的直角三角形
专题:
分析:(1)根据DE⊥BC,DF⊥AB,且DE=DF,即可得出点D在∠ABC的角平分线上,由∠ABC=60°,即可得出∠DBC=30°;
(2)根据在直角三角形中,含30°角的直角边等于斜边的一半,即可得出DF的长.
(2)根据在直角三角形中,含30°角的直角边等于斜边的一半,即可得出DF的长.
解答:解:(1)∵DE⊥BC,DF⊥AB,且DE=DF,
∴BD平分∠ABC,
∵∠ABC=60°,
∴∠DBC=30°;
(2)∵BD平分∠ABC,
∴∠ABD=∠DBC=30°;
∵BD=16,
∴DF=
BD=
×16=8.
∴BD平分∠ABC,
∵∠ABC=60°,
∴∠DBC=30°;
(2)∵BD平分∠ABC,
∴∠ABD=∠DBC=30°;
∵BD=16,
∴DF=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了角平分线的性质以及含30度角的直角三角形的性质,在直角三角形中,含30°角的直角边等于斜边的一半.

练习册系列答案
相关题目
代数式
有意义的条件( )
| 1 | ||
|
| A、x≠-1 | B、x>-1 |
| C、x≥-1 | D、x>1 |

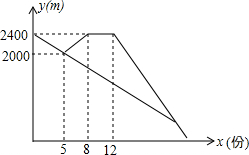 小明和爸爸从家一起出发,沿相同的路线以相同的速度步行去体育馆看球赛,途中发现忘带球票,小明立即以更快的速度跑步返回家取票,爸爸继续以原来的速度步行前往体育馆.小明上楼取票用了几分钟后骑自行车沿原来的路线骑向体育馆,小明追上爸爸后用自行车带着爸爸一起前往体育馆,自行车的速度是出发时步行速度的3倍.如图是小明和爸爸距体育馆的路程y(米)与出发的时间x(分)的函数图象.根据图象解答下列问题.
小明和爸爸从家一起出发,沿相同的路线以相同的速度步行去体育馆看球赛,途中发现忘带球票,小明立即以更快的速度跑步返回家取票,爸爸继续以原来的速度步行前往体育馆.小明上楼取票用了几分钟后骑自行车沿原来的路线骑向体育馆,小明追上爸爸后用自行车带着爸爸一起前往体育馆,自行车的速度是出发时步行速度的3倍.如图是小明和爸爸距体育馆的路程y(米)与出发的时间x(分)的函数图象.根据图象解答下列问题. 在对口扶贫活动中,企业甲将经营状况良好的某消费品专卖店,以5.8万元的优惠价转让给了尚有5万元无息贷款还没有偿还的小型残疾人企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支4000元后,逐步偿还转让费(不计利息)从企业甲提供的相关资料中可知这种消费品的进价是每件12元;月销售量Q(百件)与销售单价P(元)的关系如图所示,但销售量受市场需求量的限制,维持企业的正常运转每月需最低生活费外的各种开支2000元.
在对口扶贫活动中,企业甲将经营状况良好的某消费品专卖店,以5.8万元的优惠价转让给了尚有5万元无息贷款还没有偿还的小型残疾人企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支4000元后,逐步偿还转让费(不计利息)从企业甲提供的相关资料中可知这种消费品的进价是每件12元;月销售量Q(百件)与销售单价P(元)的关系如图所示,但销售量受市场需求量的限制,维持企业的正常运转每月需最低生活费外的各种开支2000元. 如图,△ABD、△BCD都是等边三角形,E、F分别是AD、CD上的两个动点,且满足DE=CF.求证:BE=BF.
如图,△ABD、△BCD都是等边三角形,E、F分别是AD、CD上的两个动点,且满足DE=CF.求证:BE=BF. 如图,在△ABC中,∠B=22.5°,∠C=60°,线段AB的垂直平分线FD分别交BC,AB于点D,F,AE⊥BC,垂足为点E,EC=2
如图,在△ABC中,∠B=22.5°,∠C=60°,线段AB的垂直平分线FD分别交BC,AB于点D,F,AE⊥BC,垂足为点E,EC=2