题目内容
已知一次函数y=
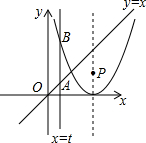
x+2的图象与二次函数y=ax2+bx+c的图象交于y轴上一点A,二次函数y=ax2+bx+c的图象与x轴只有唯一的交点B,且OB=2,求二次函数的解析式.
| 1 |
| 2 |
考点:抛物线与x轴的交点
专题:
分析:根据y=
x+2与y轴交于点A,即可得出A点坐标,二次函数y=ax2+bx+c的图象与x轴只有唯一的交点B,且OB=2.得出可设二次函数y=ax2+bx+c=a(x-2)2,进而求出即可.
| 1 |
| 2 |
解答:解:∵y=
x+2与y轴交于点A,
∵x=0,
∴y=2
∴A点坐标为:(0,2),
∵二次函数y=ax2+bx+c的图象与x轴只有唯一的交点B,且OB=2
∴可设二次函数y=a(x-2)2或y=a(x+2)2
把A(0,2)代入得:a=
∴二次函数的解析式:y=
x2-2x+2或y=
x2+2x+2.
| 1 |
| 2 |
∵x=0,
∴y=2
∴A点坐标为:(0,2),
∵二次函数y=ax2+bx+c的图象与x轴只有唯一的交点B,且OB=2
∴可设二次函数y=a(x-2)2或y=a(x+2)2
把A(0,2)代入得:a=
| 1 |
| 2 |
∴二次函数的解析式:y=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了二次函数与坐标轴交点等知识,根据已知进行分类讨论得出所有结果,注意不要漏解.

练习册系列答案
相关题目
比x的相反数小2的数是( )
| A、-x+2 | B、-x-2 |
| C、-(x-2) | D、x-2 |
 将抛物线
将抛物线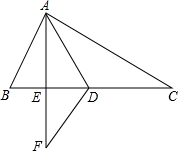 如图,D是△ABC的BC边上的一点,且CD=AB,∠BDA=∠BAD.AE是△ABD的中线,延长AE到F,使EF=AE,连接DF.求证:AE=
如图,D是△ABC的BC边上的一点,且CD=AB,∠BDA=∠BAD.AE是△ABD的中线,延长AE到F,使EF=AE,连接DF.求证:AE=