题目内容
9.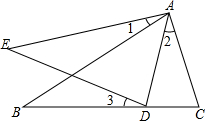 如图,已知∠1=∠2=∠3,ED=BC,试判断△ACD的形状,并说明理由.
如图,已知∠1=∠2=∠3,ED=BC,试判断△ACD的形状,并说明理由.
分析 证明△ABC≌△AED,则∠C=∠ADE,根据三角形内角和定理可证∠C=∠ADC,则AD=AC,所以△ACD是等腰三角形.
解答 解:△ACD是等腰三角形.
理由如下:∵∠1=∠2,
∴∠BAC=∠EAD,
∵∠1=∠3,
∴∠B=∠E,
在△ABC和△AED中,
$\left\{\begin{array}{l}{∠B=∠E}\\{∠BAC=∠EAD}\\{ED=BC}\end{array}\right.$,
∴△ABC≌△AED,
∴∠C=∠ADE,
∵∠3+∠ADE+∠ADC=∠ADC+∠2+∠C=180°,
∴∠ADC=∠C,
∴AD=AC,
∴△ACD是等腰三角形.
点评 本题主要考查了全等三角形的判定与性质以及等腰三角形的判定和三角形内角和定理的综合运用,熟练掌握全等三角形的判定方法是解决问题的关键.

练习册系列答案
相关题目
19.点A在数轴上表示2,一只小蚂蚁从点A沿数轴爬行4个单位长度到达B,B表示的数与A点表示的数的商为( )
| A. | -1 | B. | 3 | C. | -1或3 | D. | 1或-3 |
18.购一批水果,运输过程中损失10%,不计其他费用,要想获得至少20%的利润,则售价至少比进价提高 ( )
| A. | 34% | B. | 33.4% | C. | 33.3% | D. | 33% |
 如图所示,△ABC≌△DFE.试求∠FDB+∠ABD的值.
如图所示,△ABC≌△DFE.试求∠FDB+∠ABD的值. 若用A、B、C分别表示有理数a、b、c,0为原点如图所示,化简:|c|+|a+b|+|b-c|-|a-c|.
若用A、B、C分别表示有理数a、b、c,0为原点如图所示,化简:|c|+|a+b|+|b-c|-|a-c|.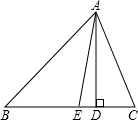 如图,在△ABC中,AD是边BC上的高,AE是∠A的角平分线,且∠C=60°,∠B=40°,求∠AED,∠EAD,∠CAD的度数.
如图,在△ABC中,AD是边BC上的高,AE是∠A的角平分线,且∠C=60°,∠B=40°,求∠AED,∠EAD,∠CAD的度数. 已知AB,CD相交于点O,且AB=CD,AD=CB,
已知AB,CD相交于点O,且AB=CD,AD=CB,