题目内容
14.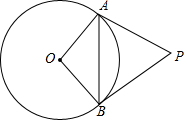 如图,PA,PB是⊙O的两条切线,A,B是切点,连接AB,已知AB=4.8,OA=3,那么PB的长度为4.
如图,PA,PB是⊙O的两条切线,A,B是切点,连接AB,已知AB=4.8,OA=3,那么PB的长度为4.
分析 连接OP,交AB于点C,利用垂径定理求得BC的长,然后利用勾股定理求得OC的长,证明△OPB∽△OBC,根据相似三角形的对应边的比相等求解.
解答 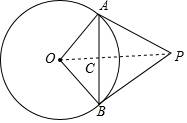 解:连接OP,交AB于点C.
解:连接OP,交AB于点C.
∵PA和PB是⊙O的两条切线,
∴PA=PB,且PO平分∠APB,
∴OP⊥AB,
∴BC=$\frac{1}{2}$AB=$\frac{1}{2}$×4.8=2.4.
∴在直角△OBC中,OC=$\sqrt{O{B}^{2}-B{C}^{2}}$=$\sqrt{{3}^{2}-2.{4}^{2}}$=1.8,
∵PB是⊙O的两条切线,
∴OB⊥PB,
∴△OPB∽△OBC,
∴$\frac{PB}{BC}$=$\frac{OB}{OC}$,即$\frac{PB}{2.4}$=$\frac{3}{1.8}$,
∴PB=4.
故答案是:4.
点评 本题考查了切线长定理以及垂径定理和相似三角形的判定与性质,正确证明△OPB∽△OBC是关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
4.正五边形的画法通常是先把圆分成五等份,然后连接五等分点而得,这种画法的理论依据应( )
| A. | 把圆n等分,顺次连接各分点得到的多边形是圆的内接正n边形 | |
| B. | 把圆n等分,依次过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形 | |
| C. | 各边相等.并且各角也相等的多边形是正多边形 | |
| D. | 用量角器等分圆是一种简单而常用的方法 |
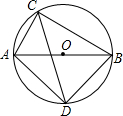 如图,AB为⊙O的直径,AC为⊙O的弦,AB=6,AC=2,∠ACB的平分线交⊙O于点D.
如图,AB为⊙O的直径,AC为⊙O的弦,AB=6,AC=2,∠ACB的平分线交⊙O于点D.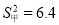 ,乙同学的方差是
,乙同学的方差是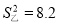 ,那么这两名同学跳高成绩比较稳定的是_____同学.
,那么这两名同学跳高成绩比较稳定的是_____同学.