题目内容
9.一队学生到校外进行野营训练,他们以5千米/时的速度行进,走了18分钟的时候,学校要将一个紧急通知传给队长,通讯员从学校出发,骑自行牢以14千米/小时的速度按原路追赶队伍.(1)问通讯员用多长时间可以追上队伍?
(2)若要求通讯员在6分钟内把通知送到队长手中,那么通讯员至少应以怎样的速度行进(不考虑队伍长度)?
分析 (1)可设通讯员需x小时可以追上队伍,根据等量关系:通讯员所走的路程=学生所走的路程,列出方程,求解即可;
(2)设通讯员应以a千米/小时的速度行进,根据题意列出方程解答即可.
解答 解:(1)设通讯员需x小时可以追上队伍,由题意得
5×$\frac{18}{60}$+5x=14x,
解得:x=$\frac{1}{6}$.
答:通讯员需$\frac{1}{6}$小时可以追上队伍.
(2)设通讯员应以a千米/小时的速度行进,由题意得
$\frac{6}{60}$a=5×$\frac{6+18}{60}$,
解得:a=20.
答:设通讯员应至少以20千米/小时的速度行进.
点评 此题考查一元一次方程的实际运用,掌握行程问题中基本数量关系是解决问题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
19.抛物线y=2(x-3)2+1的顶点坐标是( )
| A. | (3,1) | B. | (-3,1) | C. | (1,-3) | D. | (1,3) |
20.有下列条件:①∠AOP=∠BOP;②∠AOP=$\frac{1}{2}∠AOB$;③∠BOP=$\frac{1}{2}∠AOB$④∠AOB=2∠AOP.其中一定能推出OP是∠AOB的平分线的条件有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
4.使等式$\frac{7}{{x}^{2}-2}$=$\frac{7x}{{x}^{3}-2x}$从左到右的变形成立的条件是( )
| A. | x<0 | B. | x>0 | C. | x≠0 | D. | x为任意实数 |
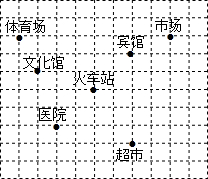 如图,这是某城市部分简图,每个小正方形的边长为1个单位长度,已知火车站的坐标为(1,2),试建立平面直角坐标系,并分别写出其它各地点的坐标.
如图,这是某城市部分简图,每个小正方形的边长为1个单位长度,已知火车站的坐标为(1,2),试建立平面直角坐标系,并分别写出其它各地点的坐标.