题目内容
14.已知三角形ABC中,AB=$\sqrt{2}$,∠A=45度,cosA、cosC是方程4x2-2(1+$\sqrt{2}$)x+m=0的两个根.求:(1)∠B的度数;
(2)m的值;
(3)AC边的长.
分析 (1)利用特殊角的三角函数值得到cosA=$\frac{\sqrt{2}}{2}$,再根据根与系数的关系得cosA+cosC=-$\frac{-2(1+\sqrt{2})}{4}$,则可计算出cosC=$\frac{1}{2}$,所以∠C=60°,然后利用三角形内角和求∠B的度数;
(2)根据根与系数的关系得cosA•cosC=$\frac{m}{4}$,所以m=2$\sqrt{2}$+2;
(3)如图,作BD⊥AC于D,先利用△ABD为等腰直角三角形得到AD=BD=$\frac{\sqrt{2}}{2}$AB=1,再在Rt△BDC中,利用∠C=60°得到=$\frac{\sqrt{3}}{3}$BD=$\frac{\sqrt{3}}{3}$,然后计算AD+CD即可.
解答 解:(1)∵∠A=45度,
∴cosA=cos45°=$\frac{\sqrt{2}}{2}$,
∵cosA+cosC=-$\frac{-2(1+\sqrt{2})}{4}$,
∴$\frac{\sqrt{2}}{2}$+cosC=$\frac{1+\sqrt{2}}{2}$,
∴cosC=$\frac{1}{2}$,
∴∠C=60°,
∴∠B=180°-45°-60°=75°;
(2)∵cosA•cosC=$\frac{m}{4}$,
∴m=4($\frac{\sqrt{2}}{2}$+$\frac{1}{2}$)=2$\sqrt{2}$+2;
(3)如图,作BD⊥AC于D,
∵∠A=45°,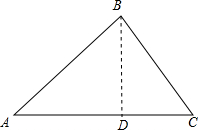
∴△ABD为等腰直角三角形,
∴AD=BD=$\frac{\sqrt{2}}{2}$AB=$\frac{\sqrt{2}}{2}$×$\sqrt{2}$=1,
在Rt△BDC中,∵∠C=60°,
∴CD=$\frac{\sqrt{3}}{3}$BD=$\frac{\sqrt{3}}{3}$,
∴AC=AD+CD=1+$\frac{\sqrt{3}}{3}$.
点评 本题考查了一元二次方程的应用:列方程解决实际问题的一般步骤是:审清题意设未知数,列出方程,解所列方程求所列方程的解,检验和作答.也考查了根与系数的关系和解直角三角形.

| A. | 2cm,3cm,3cm | B. | 4cm,4cm,4cm | C. | 3cm,4cm,7cm | D. | 1cm,$\sqrt{2}$cm,$\sqrt{3}$cm |
| A. | y=x2+2 | B. | y=-(x+1)2+3 | C. | y=-3(x+1)2+3 | D. | y=-3(x-1)2+3 |
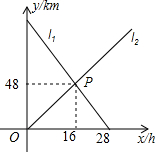 如图,小明从A地出发向B地行走,同时小亮从B地出发向A地行走,线段l1,l2分别表示小明、小亮离B地的距离与已用时间之间的关系,当x=0.5或2.7h时,小明与小亮相距7.7km.
如图,小明从A地出发向B地行走,同时小亮从B地出发向A地行走,线段l1,l2分别表示小明、小亮离B地的距离与已用时间之间的关系,当x=0.5或2.7h时,小明与小亮相距7.7km.