题目内容
19．小丽家在铺设地板时，用的是边长相等的三种正多边形，已知第一种正多边形的一个内角是120°，另一种是正方形，而且铺地板时，在一个顶点处，这三种正多边形都是一个，则第三种正多边形应是正12边形．分析 正多边形的组合能否进行平面镶嵌，关键是看位于同一顶点处的几个角之和能否为360°．若能，则说明可以进行平面镶嵌；反之，则说明不能进行平面镶嵌．
解答 解：∵正方形的一个内角度数为180°-360°÷4=90°，正六边形的一个内角度数为180°-360°÷6=120°，
∴需要的多边形的一个内角度数为360°-90°-120°=150°，
∴需要的多边形的一个外角度数为180°-150°=30°，
∴第三个正多边形的边数为360÷30=12．
故答案为：12．
点评 此题主要考查了平面镶嵌，关键是掌握多边形镶嵌成平面图形的条件：同一顶点处的几个内角之和为360°；正多边形的边数为360÷一个外角的度数．
练习册系列答案
相关题目
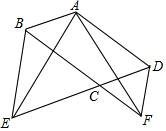如图，在?ABCD中，∠BCD=120°，分别以BC和CD为边作等边△BCE和等边△CDF．
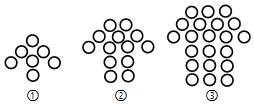下列图形都是由两样大小的小圆圈按一定规律组成的，其中第①个图形中一共有7个小圆圈，第②个图形中一共有13个小圆圈，第③个图形中一共有21个小圆圈，…，按此规律排列，则第⑧个图形中小圆圈的个数为（ ）
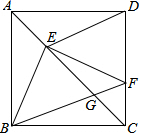如图，正方形ABCD的边长为1，点E、F分别在AC、DC上，若EC=BC，EF⊥BE，BF与EC交于点G，则$\frac{EG}{CG}$=$\sqrt{2}$．
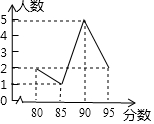在一次“班班有诗词”竞赛活动中，某班10名学生的成绩折线统计图如图所示，若随机从这10名学生中抽取一人，则抽中概率最大的学生得分是90分．