题目内容
10.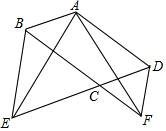 如图,在?ABCD中,∠BCD=120°,分别以BC和CD为边作等边△BCE和等边△CDF.
如图,在?ABCD中,∠BCD=120°,分别以BC和CD为边作等边△BCE和等边△CDF.求证:AE=AF.
分析 根据平行四边形的性质得出AB=CD,BC=AD,∠ABC=∠ADC,根据等边三角形的性质得出DC=DF,BC=BE,∠EBC=∠CDF=60°,求出AB=DF,BE=DA,∠ABE=∠FDA,根据SAS推出△ABE≌△FDA即可.
解答 证明:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,∠ABC=∠ADC,
∵△BCE和△CDF为等边三角形,
∴DC=DF,BC=BE,∠EBC=∠CDF=60°,
∴AB=DF,BE=DA,∠ABE=∠FDA,
在△ABE和△FDA中,$\left\{\begin{array}{l}{AB=DF}&{\;}\\{∠ABE=∠FDA}&{\;}\\{BE=AD}&{\;}\end{array}\right.$,
∴△ABE≌△FDA(SAS),
∴AE=AF.
点评 本题考查了平行四边形的性质,全等三角形的性质和判定,等边三角形的性质的应用,能综合运用定理进行推理是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=22°,那么∠2的度数是( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=22°,那么∠2的度数是( )
 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=22°,那么∠2的度数是( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=22°,那么∠2的度数是( )| A. | 22° | B. | 78° | C. | 68° | D. | 70° |
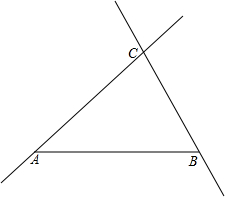 如图,公路AC、BC分别经过A、B两个工厂,现想修建一个货物中转站P,使它到两条公路AC、BC的距离相等,并且到A、B两个工厂的距离也相等.请你利用尺规确定货物中转站P的位置.(保留作图痕迹,不写作法)
如图,公路AC、BC分别经过A、B两个工厂,现想修建一个货物中转站P,使它到两条公路AC、BC的距离相等,并且到A、B两个工厂的距离也相等.请你利用尺规确定货物中转站P的位置.(保留作图痕迹,不写作法)