题目内容
17.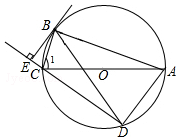 如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,过点B作⊙O的切线交DC的延长线于点E.
如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,过点B作⊙O的切线交DC的延长线于点E.(1)求证:∠1=∠BAD;
(2)求证:BE⊥DC.
分析 (1)由弦BD=BA,可得∠BAD=∠BDA,又由圆周角定理可得∠1=∠ADB,继而证得结论;
(2)首先连接OB,由BE是⊙O的切线,可得OB⊥BE,又由∠1=∠OBC=∠BDA=∠BAD,易得∠BOC=∠ACD,继而证得OB∥CD,则可证得结论.
解答 证明:(1)∵弦BD=BA,
∴∠BDA=∠BAD,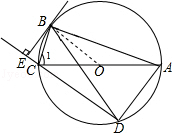
∵∠1=∠BDA,
∴∠1=∠BAD;
(2)连接OB,
∵BE是⊙O的切线,
∴OB⊥BE,
∵OB=OC,
∴∠1=∠OBC,
∴∠1=∠OBC=∠BDA=∠BAD,
∴∠BOC=∠ABD,
∵∠ABD=∠ACD,
∴∠BOC=∠ACD,
∴OB∥CD,
∴BE⊥CD.
点评 此题考查了切线的性质以及圆周角定理.注意准确作出辅助线是解此题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
7.满足-$\sqrt{2}$<x<$\sqrt{5}$的整数x是( )
| A. | -1,0,1,2 | B. | -2,-1,0,1 | C. | -1,1,2,3 | D. | 0,1,2,3 |
8.已知三角形三边长分别为2,2x,13,若x为正整数,则这样的三角形个数为( )
| A. | 2 | B. | 3 | C. | 5 | D. | 13 |
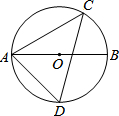 如图,AB为⊙O的直径,点C在⊙O上,且∠CAB=30°,点D为弧$\widehat{AB}$的中点,AC=4$\sqrt{3}$.求AD的长.
如图,AB为⊙O的直径,点C在⊙O上,且∠CAB=30°,点D为弧$\widehat{AB}$的中点,AC=4$\sqrt{3}$.求AD的长.