题目内容
2.已知x+y=$\sqrt{\sqrt{2017}+\sqrt{2016}}$,x-y=$\sqrt{\sqrt{2017}-\sqrt{2016}}$,则:(1)x2-y2=1
(2)x4-y4=$\sqrt{2017}$.
分析 结合二次根式的概念进行求解即可.
解答 解:(1)x2-y2
=(x+y)(x-y)
=$\sqrt{\sqrt{2017}+\sqrt{2016}}$×$\sqrt{\sqrt{2017}-\sqrt{2016}}$
=$\sqrt{2017-2016}$
=1.
(2)x4-y4
=(x2-y2)(x2+y2)
=(x2+y2)
=(x+y)2-2xy
=(x+y)2-2[$\frac{1}{4}$(x+y)2-(x-y)2]
=$\sqrt{2017}$+$\sqrt{2016}$-$\frac{1}{2}$(2$\sqrt{2016}$)
=$\sqrt{2017}$.
故答案为;(1)1,(2)$\sqrt{2017}$.
点评 本题考查了二次根式的化简求值,解答本题的关键在于熟练掌握平方差公式及完全平方公式.

练习册系列答案
相关题目
7.满足-$\sqrt{2}$<x<$\sqrt{5}$的整数x是( )
| A. | -1,0,1,2 | B. | -2,-1,0,1 | C. | -1,1,2,3 | D. | 0,1,2,3 |
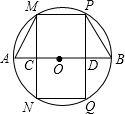 如图,AB是⊙O直径,C、D是AB上两点,MC⊥AB交⊙O于M、N,PD⊥AB交⊙O于P、Q,
如图,AB是⊙O直径,C、D是AB上两点,MC⊥AB交⊙O于M、N,PD⊥AB交⊙O于P、Q,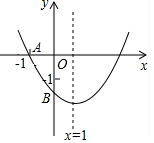 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac-b2<16a;④$\frac{1}{3}$<a<$\frac{2}{3}$;⑤b>c.
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac-b2<16a;④$\frac{1}{3}$<a<$\frac{2}{3}$;⑤b>c. 二次函数y=-3x2+1的图象如图所示,将其沿x轴翻折后得到的抛物线的解析式为y=3x2-1.
二次函数y=-3x2+1的图象如图所示,将其沿x轴翻折后得到的抛物线的解析式为y=3x2-1. 如图是几个小立方块所搭几何体的俯视图,小正方形的数字表示该位置小立方块的个数.请画出这个几何体的主视图和左视图.
如图是几个小立方块所搭几何体的俯视图,小正方形的数字表示该位置小立方块的个数.请画出这个几何体的主视图和左视图.