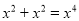题目内容
△ABC和△ADE都是等腰直角三角形, ∠BAC=∠DAE=90°.
(1)如图1,点D,E在AB,AC上,则BD,CE满足怎样的数量关系和位置关系?(直接写出答案)
(2)如图2,点D在△ABC内部, 点E在△ABC外部,连结BD, CE, 则BD,CE满足怎样的数量关系和位置关系?请说明理由.
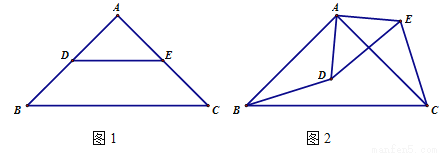
(3)如图3,点D,E都在△ABC外部,连结BD, CE, CD, EB,BD, 与CE相交于H点.
①若BD=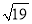 ,求四边形BCDE的面积;
,求四边形BCDE的面积;
②若AB=3,AD=2,设CD2=x,EB2=y,求y与x之间的函数关系式.

练习册系列答案
相关题目


 中,
中, 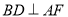 ,
, 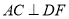 ,点
,点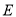 、
、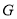 分别为
分别为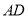 、
、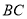 中点.
中点.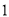 )若
)若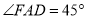 ,
, 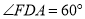 ,求
,求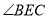 的度数;
的度数;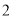 )试判断
)试判断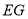 与
与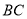 的位置关系,并说明理由.
的位置关系,并说明理由.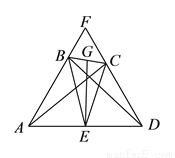

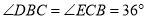 ,
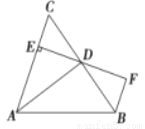
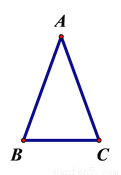
,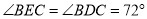 ,则图中等腰三角形的个数是
,则图中等腰三角形的个数是
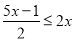 ;(2)
;(2)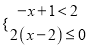
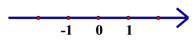

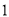 )
)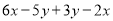 ,其中
,其中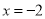 ,
, 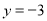 .
.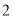 )
)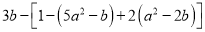 ,其中
,其中 ,
, 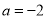 .
.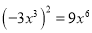 B.
B. 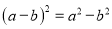 C.
C. 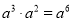 D.
D.