题目内容
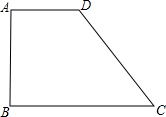 如图,有一块四边形菜地ABCD,AD∥BC.测得AB=4m,BC=6m,CD=5m,AD=3m,求菜地的面积S四边形ABCD.
如图,有一块四边形菜地ABCD,AD∥BC.测得AB=4m,BC=6m,CD=5m,AD=3m,求菜地的面积S四边形ABCD.考点:梯形,矩形的判定与性质
专题:
分析:过D作DE∥AB交BC于点E,根据已知条件可得四边形ABED是矩形,所以菜地的面积可转化为矩形的面积和三角形DEC的面积和.
解答:解:过D作DE∥AB交BC于点E,
∵AD∥BC,
∴四边形ABED是平行四边形,
∴DE=AB=4,BE=AD=3,
∵CE=BC-BE=3,
∴DE2+CE2=DC2,
∴DE⊥BC,
∴四边形ABED是矩形,
∴S四边形ABCD=4×3+
×3×4=18m2.

∵AD∥BC,
∴四边形ABED是平行四边形,
∴DE=AB=4,BE=AD=3,
∵CE=BC-BE=3,
∴DE2+CE2=DC2,
∴DE⊥BC,
∴四边形ABED是矩形,
∴S四边形ABCD=4×3+
| 1 |
| 2 |
点评:本题考查了梯形的性质、矩形的判定和性质以及勾股定理逆定理的运用,解题的关键是正确做出辅助线,构造直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在平面直角坐标系中,O为坐标原点.已知A(0,a)B(b,b),C(c,a),其中a、b满足关系式|a-4|+(b-2)2=0,c=a+b.
在平面直角坐标系中,O为坐标原点.已知A(0,a)B(b,b),C(c,a),其中a、b满足关系式|a-4|+(b-2)2=0,c=a+b. 已知:如图,点E,F是?ABCD中AB,DC边上的点,且AE=CF,联结DE,BF.求证:DE=BF.
已知:如图,点E,F是?ABCD中AB,DC边上的点,且AE=CF,联结DE,BF.求证:DE=BF. 如图,在直角三角形△ABC中,CD是斜边AB上的高,∠A=35°.求:
如图,在直角三角形△ABC中,CD是斜边AB上的高,∠A=35°.求: