题目内容
4.已知抛物线y=3(x-2)2+k(k为常数),A(-3,y1),B(3,y2),C(4,y3)是抛物线上三点,则y1,y2,y3由小到大依序排列为( )| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y2<y3<y1 | D. | y3<y2<y1 |
分析 先求出二次函数y=3(x-2)2+k的图象的对称轴,然后判断出A(-3,y1),B(3,y2),C(4,y3)在抛物线上的位置,再求解.
解答 解:∵二次函数y=3(x-2)2+k中a=3>0
∴抛物线开口向上,对称轴为x=-$\frac{b}{2a}$=2,
∵B(3,y2),C(4,y3)中横坐标均大于2,
∴它们在对称轴的右侧y3>y2.
A(-3,y1)中横坐标小于2,
∵它在对称轴的左侧,它关于x=2的对称点为2×2-(-3)=7,
A点的对称点是D(7,y1)
7>4>3,
∵a>0时,抛物线开口向上,在对称轴的右侧y随x的增大而增大,
∴y1>y3>y2.
故选:C.
点评 本题考查了二次函数图象上点的坐标特征,本题的关键是找到A点的对称点;掌握二次函数y=ax2+bx+c(a≠0)的图象性质.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
15.下列等式是一元一次方程的是( )
| A. | x2+3x=6 | B. | 2x=4 | C. | -$\frac{1}{2}$x-y=0 |
12.下面①②③④用拼图法验证“三角形内角和为180°”,能成为证明这个定理思路的有( )


| A. | ①②③④ | B. | ①③ | C. | ③④ | D. | ①② |
19. 如图,⊙O的半径为3,正六边形ABCDEF内接于⊙O,则劣弧AC的长为( )
如图,⊙O的半径为3,正六边形ABCDEF内接于⊙O,则劣弧AC的长为( )
 如图,⊙O的半径为3,正六边形ABCDEF内接于⊙O,则劣弧AC的长为( )
如图,⊙O的半径为3,正六边形ABCDEF内接于⊙O,则劣弧AC的长为( )| A. | 6π | B. | 3π | C. | 2π | D. | π |
9.某小区9月底的房价为3.2万元/m2,同年11月底的房价为3万元/m2.设平均每月降价的百分率为 x,可列方程.( )
| A. | 3.2(1+x)2=3 | B. | 3.2(1-x)2=3 | C. | 3(1+x)2=3.2 | D. | 3(1-x)2=3.2 |
16.下列各数是无理数的为( )
| A. | -9 | B. | $\frac{π}{3}$ | C. | 4.121121112 | D. | $\frac{22}{7}$ |
13.下列事件中,是必然事件的是( )
| A. | 打开电视机,它正在直播排球比赛 | |
| B. | 抛掷5枚硬币,结果是2个正面朝上与3个反面朝上 | |
| C. | 黑暗中从一大串钥匙中随便选中一把,用它打开了门 | |
| D. | 投掷一枚普通的正方体骰子,正面朝上的数不是奇数便是偶数 |
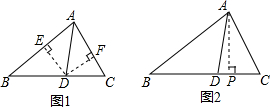 让我们来共同探究“三角形的角平分线”的特殊性质:
让我们来共同探究“三角形的角平分线”的特殊性质: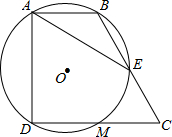 如图,已知直角梯形ABCD中,∠BAD=∠CDA=90°,CD=2AB,过A、B、D三点的⊙O分别交BC、CD于E、M.
如图,已知直角梯形ABCD中,∠BAD=∠CDA=90°,CD=2AB,过A、B、D三点的⊙O分别交BC、CD于E、M.