题目内容
13.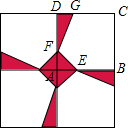 一个边长为8m的正方形花坛由4块全等的小正方形组成,在小正方形ABCD中,点G、E、F分别在CD、AB、AD上,且DG=1m,AE=AF,在△AEF、△DFG、五边形EBCGF三个区域上种植不同的花卉,每平方米的种植成本分别是20元、20元、10元,问点E在什么位置时,正方形花坛种植花卉所需的总费用是715元?
一个边长为8m的正方形花坛由4块全等的小正方形组成,在小正方形ABCD中,点G、E、F分别在CD、AB、AD上,且DG=1m,AE=AF,在△AEF、△DFG、五边形EBCGF三个区域上种植不同的花卉,每平方米的种植成本分别是20元、20元、10元,问点E在什么位置时,正方形花坛种植花卉所需的总费用是715元?
分析 设AE=AF=x米,则DF=(4-x)米.先求出△AEF和△DFG的面积,再得到五边形EFBCG的面积,然后根据正方形花坛种植花卉所需的总费用是715元列出方程,解方程即可.
解答 解:设AE=AF=x米,则DF=(4-x)米.
S△AEF=$\frac{1}{2}$AE×AF=$\frac{1}{2}$x2,S△DFG=$\frac{1}{2}$DG×DF=$\frac{1}{2}$×1×(4-x)=2-$\frac{1}{2}$x,
S五边形EBCGF=S正方形ABCD-S△AEF-S△DFG=16-$\frac{1}{2}$x2-2+$\frac{1}{2}$x=-$\frac{1}{2}$x2+$\frac{1}{2}$x+14,
根据题意得4×[20×$\frac{1}{2}$x2+20×(2-$\frac{1}{2}$x)+10×(-$\frac{1}{2}$x2+$\frac{1}{2}$x+14)]=715,
整理得4x2-4x+1=0,
解得x1=x2=$\frac{1}{2}$.
答:当AE=AF=$\frac{1}{2}$米时,正方形花坛种植花卉所需的总费用是715元.
点评 本题考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
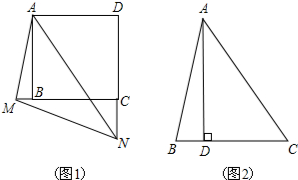
 如图,在△ABC中,D是AC的中点,E,F在BC上,且BE=EF=FC,AE与BD交于点M,G是AE的中点,DF与CG交于点N,求证:MN∥BC.
如图,在△ABC中,D是AC的中点,E,F在BC上,且BE=EF=FC,AE与BD交于点M,G是AE的中点,DF与CG交于点N,求证:MN∥BC.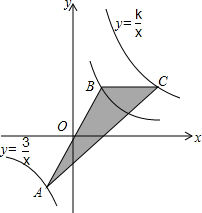 如图,点A在双曲线y=$\frac{3}{x}$第三象限的分支上,连结AO并延长交第一象限的图象于点B,画BC∥x轴交反比例函数y=$\frac{k}{x}$的图象于点C,若△ABC的面积为6,则k的值是9.
如图,点A在双曲线y=$\frac{3}{x}$第三象限的分支上,连结AO并延长交第一象限的图象于点B,画BC∥x轴交反比例函数y=$\frac{k}{x}$的图象于点C,若△ABC的面积为6,则k的值是9.