题目内容
18.若不等式组$\left\{\begin{array}{l}{2x-b≥0}\\{x+a≤0}\end{array}\right.$的解集为3≤x≤4,求不等式ax+b<0的解集.分析 首先计算出a、b的值,然后可得不等式-2x+1<0,再解不等式即可.
解答 解:$\left\{\begin{array}{l}{2x-b≥0①}\\{x+a≤0②}\end{array}\right.$,
由①得:x≥$\frac{b}{2}$,
由②得:x≤-a,
∵解集是3≤x≤4,
∴$\left\{\begin{array}{l}{\frac{b}{2}=3}\\{-a=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-4}\\{b=6}\end{array}\right.$,
∴不等式ax+b<0变为-4x+6<0,
解得:x>$\frac{3}{2}$.
点评 此题主要考查了解一元一次不等式组,以及解一元一次不等式,关键是计算出a、b的值.

练习册系列答案
相关题目
10.某农场计划安排10个生产组来耕作30公顷土地,这些土地可以种蔬菜,也可以种水稻,种这些作物所需生产组及预计产值如表:
为了使所有土地都种上作物,且全部生产组都有工作,应安排多少个生产组种蔬菜?这时预计总产值为多少元?
| 每公顷所需生产组/个 | 每公顷雨季产值 | |
| 蔬菜 | $\frac{1}{2}$ | 52500 |
| 水稻 | $\frac{1}{4}$ | 18000 |
8.体育文化用品店购进篮球和排球共40个,进价和售价如表,全部售完后共获利520元.
(1)购进篮球和排球各多少个?
(2)销售时,用6000元买了50个篮球和若干个排球,能获得利润多少?
| 篮球 | 排球 | |
| 进价(元/个) | 80 | 50 |
| 售价(元/个) | 95 | 60 |
(2)销售时,用6000元买了50个篮球和若干个排球,能获得利润多少?
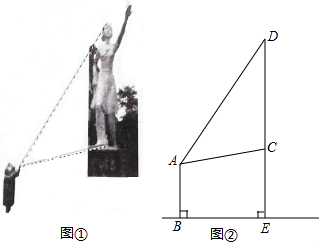
 如图,已知线段a和b,a>b,求作直角三角形ABC,使直角三角形的斜边AB=a,直角边AC=b.(用尺规作图,保留作图痕迹,不要求写作法)
如图,已知线段a和b,a>b,求作直角三角形ABC,使直角三角形的斜边AB=a,直角边AC=b.(用尺规作图,保留作图痕迹,不要求写作法)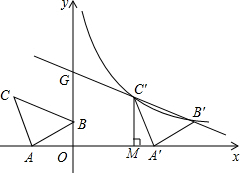 如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,d)、C(-3,2).
如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,d)、C(-3,2).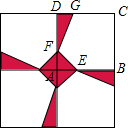 一个边长为8m的正方形花坛由4块全等的小正方形组成,在小正方形ABCD中,点G、E、F分别在CD、AB、AD上,且DG=1m,AE=AF,在△AEF、△DFG、五边形EBCGF三个区域上种植不同的花卉,每平方米的种植成本分别是20元、20元、10元,问点E在什么位置时,正方形花坛种植花卉所需的总费用是715元?
一个边长为8m的正方形花坛由4块全等的小正方形组成,在小正方形ABCD中,点G、E、F分别在CD、AB、AD上,且DG=1m,AE=AF,在△AEF、△DFG、五边形EBCGF三个区域上种植不同的花卉,每平方米的种植成本分别是20元、20元、10元,问点E在什么位置时,正方形花坛种植花卉所需的总费用是715元?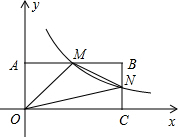 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,反比例函数y=$\frac{k}{x}$的图象经过点M,N,若M是AB的中点,△OMN的面积为3.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,反比例函数y=$\frac{k}{x}$的图象经过点M,N,若M是AB的中点,△OMN的面积为3.