题目内容
6．
如图，点O在∠APB的平分线PN上，以点O为圆心的⊙O分别交直线PN于点M、N，那么$\widehat{AM}$与$\widehat{BM}$相等吗？并说明理由．
分析 依题意得到：MN是直径，则$\widehat{AM}$+$\widehat{AN}$=$\widehat{BM}$+$\widehat{BN}$，欲证明$\widehat{AM}$=$\widehat{BM}$，只需推知$\widehat{AN}$=$\widehat{BN}$．
解答 
解：$\widehat{AM}$与$\widehat{BM}$相等，理由如下：
由题意知，MN是直径．
则$\widehat{AM}$+$\widehat{AN}$=$\widehat{BM}$+$\widehat{BN}$，
∴点O在∠APB的平分线PN上，AP=BP，
∴∠AON=∠BON，
∴$\widehat{AN}$=$\widehat{BN}$，
∴$\widehat{AM}$=$\widehat{BM}$．
点评 本题考查了圆周角、弧、弦的关系．正确理解和使用圆心角、弧、弦三者的关系：在同圆或等圆中，①圆心角相等，②所对的弧相等，③所对的弦相等，三项“知一推二”，一项相等，其余二项皆相等．这源于圆的旋转不变性，即：圆绕其圆心旋转任意角度，所得图形与原图形完全重合．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
如图，某学校教学楼前有一个边长为40m的正方形广场，学校准备在其中心建一个半径为10m的圆形花坛，在四个角落处分别建一个正方形花坛，每个小正方形花坛完全一样，其余部分铺设地砖，要求铺设地砖的区域占总面积的$\frac{9}{16}$．（π取3）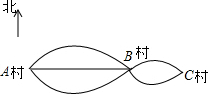
如图，从A村去B村有3条道路，从B村去C村有2条道路．
已知a，b，c在数轴上的位置如图所示，求$\frac{a}{|ab|}+\frac{1}{|b|}-\frac{3bc}{|bc|}$的值．
如图，用R表示足球的半径，球的表面积公式为S=4πR2．如果做一个足球需要的橡胶布的面积为1936π cm2，则足球的半径R为多少？