题目内容
16.求证:代数式$\frac{x-19}{\sqrt{x-3}-4}$-$\frac{x-28}{\sqrt{x-3}+5}$的值的大小与x的取值无关.分析 把分子利用平方差公式因式分解,约分后化简即可得出答案.
解答 证明:∵$\frac{x-19}{\sqrt{x-3}-4}$-$\frac{x-28}{\sqrt{x-3}+5}$
=$\frac{(\sqrt{x-3}+4)(\sqrt{x-3}-4)}{\sqrt{x-3}-4}$-$\frac{(\sqrt{x-3}+5)(\sqrt{x-3}-5)}{\sqrt{x-3}+5}$
=$\sqrt{x-3}$+4-$\sqrt{x-3}$+5
=9,
∴代数式$\frac{x-19}{\sqrt{x-3}-4}$-$\frac{x-28}{\sqrt{x-3}+5}$的值的大小与x的取值无关.
点评 此题考查二次根式的化简求值,利用平方差公式分解因式是解决问题的关键.

练习册系列答案
相关题目
11.对于近似数1.2300×105叙述正确的是( )
| A. | 精确到万分位 | B. | 精确到0.0001 | ||
| C. | 精确到精确到十位 | D. | 精确到个位 |
 如图,点O在∠APB的平分线PN上,以点O为圆心的⊙O分别交直线PN于点M、N,那么$\widehat{AM}$与$\widehat{BM}$相等吗?并说明理由.
如图,点O在∠APB的平分线PN上,以点O为圆心的⊙O分别交直线PN于点M、N,那么$\widehat{AM}$与$\widehat{BM}$相等吗?并说明理由.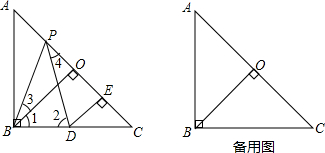
 如图,周长为46cm的长方形,把长截去5cm剩余的面积S1刚好比把宽截去5cm剩余的面积S2多35cm2,求原长方形的面积.
如图,周长为46cm的长方形,把长截去5cm剩余的面积S1刚好比把宽截去5cm剩余的面积S2多35cm2,求原长方形的面积.