题目内容
2．下列说法正确的是（ ）| A． | 如果两个三角形全等，则它们是关于某条直线成轴对称的图形 | |
| B． | 如果两个三角形关于某条直线成轴对称，那么它们是全等三角形 | |
| C． | 等边三角形是关于一条边上的中线成轴对称的图形 | |
| D． | 一条线段是关于经过该线段中点的中线成轴对称的图形 |
分析 A、因为关于某条直线成轴对称的三角形对折后能重合，所以两个三角形全等不能达到这一要求，所以此选项不正确；
B、这是成轴对称图形的性质：如果两个三角形关于某条直线成轴对称，那么它们是全等三角形；
C、等边三角形有三条对称轴，每一条边的中线所在的直线都是它的对称轴；
D、线段是成轴对称的图形，它的对称轴是这条线段的中垂线．
解答 解：A、如果两个三角形全等，则它们不一定是关于某条直线成轴对称的图形，所以选项A不正确；
B、如果两个三角形关于某条直线成轴对称，那么它们是全等三角形，所以选项B正确；
C、三角形的中线是线段，而对称轴是直线，应该说等边三角形是关于一条边上的中线所在直线成轴对称的图形，所以选项C不正确；
D、一条线段是关于经过该线段中垂线成轴对称的图形，所以选项D不正确；
故选B．
点评 本题考查了轴对称和轴对称图形的性质，熟练掌握：①如果两个图形成轴对称，那么这两个图形全等；②如果两个图形关于某直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线；③线段、等腰三角形、等边三角形等都是轴对称图形．
练习册系列答案
相关题目
已知点O是△ABC的外心，∠A=α，求∠BOC的大小．
13．已知抛物线y=-（x+1）2+m经过点A（0，3），它的解析式为（ ）
| A． | y=-（x-1）2+4 | B． | y=-（x+1）2+3 | C． | y=-（x+1）2-3 | D． | y=-（x+1）2+4 |
如图所示，在△ABC中，AB=CB，∠ABC=90°，∠CAB=∠ACB，F为AB延长线上一点，点E在BC上，且∠EAB=∠FCB．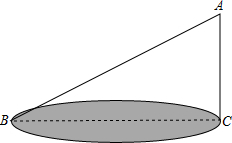
公园有三个景点A、B、C构成如图所示的直角三角形，由于B、C两景点之间有一山相隔，为方便游客，准备在B、C间挖条隧道．已知∠ACB=90°，AB=3千米，AC=2千米．试用计算器探索：这条隧道至少要修多少米？（精确到1米）
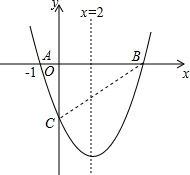如图，对称轴为直线x=2的抛物线y=x2+bx+c与x轴交于点A和点B，与y轴交于点C，且点A的坐标为（-1，0），其顶点为D．
12．
如图所示，是一个几何体的俯视图和正视图（主视图），则该几何体的表面积为（ ）
如图所示，是一个几何体的俯视图和正视图（主视图），则该几何体的表面积为（ ）| A． | （5900+400π）cm2 | B． | （5900+500π）cm2 | C． | （1600+1650π）cm2 | D． | 7500cm2 |