题目内容
9.(1)$\sqrt{45}$+$\sqrt{18}$-$\sqrt{8}$+$\sqrt{125}$;(2)在Rt△ABC中,∠ACB=90°,∠A=30°,AC=4,求AB的长.
分析 (1)根据二次根式的性质把各个二次根式化简,合并同类二次根式即可;
(2)根据余弦的概念计算即可.
解答 解:(1)原式=3$\sqrt{5}$+3$\sqrt{2}$-2$\sqrt{2}$+5$\sqrt{5}$=8$\sqrt{5}$+$\sqrt{2}$;
(2)在Rt△ABC中,AB=$\frac{AC}{cosA}$=$\frac{4}{\frac{\sqrt{3}}{2}}$=$\frac{{8\sqrt{3}}}{3}$.
点评 本题考查的是二次根式的计算、直角三角形的性质,掌握二次根式的性质、余弦的概念是解题的关键.

练习册系列答案
相关题目
17.某小组参加植树活动,全组学生的植树数量如表所示,则该小组平均每人植树7株.
| 植树数量(株) | 5 | 6 | 7 | 8 |
| 人数(人) | 1 | 1 | 2 | 3 |
4.已知在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
| A. | AD=BC | B. | AC=BD | C. | BC∥AD | D. | ∠A=∠B |
14.如图,点P在平面直角坐标系中按图中箭头方向运动,第一次从原点运动到点(1,1),第二次接着运动到点(2,0),第三次接着运动到点(3,2),…,按这样的运动规律,运动第2011次后的点坐标是 ( )
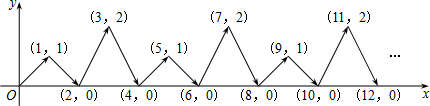

| A. | (2011,1) | B. | (2012,2) | C. | (2011,2) | D. | (2011,0) |

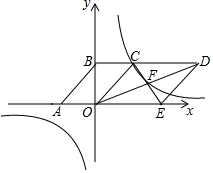 如图,已知反比例函数y=$\frac{1-m}{x}$(m为常数)的图象在平面直角坐标系的第一、三象限,且经过?ABCO的顶点C,点A,B的坐标分别为(-2,0),(0,3),若点P是该反比例函数图象上的一点,且OC=OP,则满足条件的位于第三象限内P点坐标为(-3,-2)或(-2,-3);若该反比例函数图象又经过?COED对角线的交点F,则?COED的面积为18.
如图,已知反比例函数y=$\frac{1-m}{x}$(m为常数)的图象在平面直角坐标系的第一、三象限,且经过?ABCO的顶点C,点A,B的坐标分别为(-2,0),(0,3),若点P是该反比例函数图象上的一点,且OC=OP,则满足条件的位于第三象限内P点坐标为(-3,-2)或(-2,-3);若该反比例函数图象又经过?COED对角线的交点F,则?COED的面积为18. 如图,在直角坐标系中,三角形ABC的三个顶点分别为A(-1,3)B(-4,1)C(-4,2)
如图,在直角坐标系中,三角形ABC的三个顶点分别为A(-1,3)B(-4,1)C(-4,2)