题目内容
若多项式(2mx2-x2+3x+1)-(5x2-4y2+3x)的值与x无关,求m的值?
考点:整式的加减
专题:
分析:根据去括号、合并同类项,可化简整式,根据整式与x无关,可得x、x2的系数为零,根据解方程,可得答案.
解答:解:原式=2mx2-x2+3x+1-5x2+4y2-3x
=(2m-1-5)x2+(3-3)x+4y2+1.
由多项式(2mx2-x2+3x+1)-(5x2-4y2+3x)的值与x无关,得
2m-1-5=0.
解得m=3.
=(2m-1-5)x2+(3-3)x+4y2+1.
由多项式(2mx2-x2+3x+1)-(5x2-4y2+3x)的值与x无关,得
2m-1-5=0.
解得m=3.
点评:本题考查了整式的加减,利用整式与x无关得出x的系数为零是解题关键.

练习册系列答案
相关题目
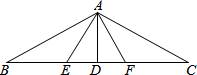 如图,在△ABC中,AB=AC,AE=AF,AD⊥BC于点D,且点E、F在BC上,则图中全等的直角三角形共有( )
如图,在△ABC中,AB=AC,AE=AF,AD⊥BC于点D,且点E、F在BC上,则图中全等的直角三角形共有( )| A、1对 | B、2对 | C、3对 | D、4对 |
下列方程是一元一次方程的是( )
| A、x-3y=4 | ||
| B、xy=4 | ||
C、
| ||
D、3y-
|
将抛物线y=-2x2+1向右平移1个单位,再向下平移3个单位后所得到的抛物线为( )
| A、y=-2(x+1)2-2 |
| B、y=-2(x+1)2-4 |
| C、y=-2(x-1)2-2 |
| D、y=-2(x-1)2-4 |
已知k>0,则一次函数y=kx-k的图象大致是( )
A、 |
B、 |
C、 |
D、 |
 如图,在直接坐标系中,已知点A(0,3),B(4,0).
如图,在直接坐标系中,已知点A(0,3),B(4,0).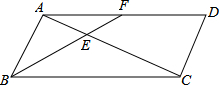 如图,在平行四边形ABCD中,点F是AD边上一点,连接BF与对角线AC相交于点E.
如图,在平行四边形ABCD中,点F是AD边上一点,连接BF与对角线AC相交于点E. 如图数轴上有点A和点B,则线段AB=
如图数轴上有点A和点B,则线段AB=