Question

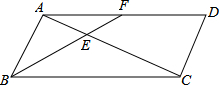如图，在平行四边形ABCD中，点F是AD边上一点，连接BF与对角线AC相交于点E．
①当

AF

AD

=

1

2

时，

S△ABF

S平行四边形ABCD

=

 

．
②当

AF

AD

=

1

2

时，

S△ABF

S平行四边形ABCD

=

 

，

S△AEF

S平行四边形ABCD

=

 

．

Answer 1

考点：相似三角形的判定与性质,平行四边形的性质

专题：

分析：①根据三角形的面积公式和平行四边形的面积公式进行解答即可；
②利用相似三角形：△AEF∽△CEB的性质来求

S△AEF

S平行四边形ABCD

的值．

解答：解：∵四边形ABCD是平行四边形，
∴AD∥BC，
∴△ABF与?ABCD同高．
①∵

AF

AD

=

1

2

，
∴

S△ABF

S平行四边形ABCD

=

1 2 AF

AD

=

1

4

．
故答案是：

1

4

．
②如图，由①知，

S△ABF

S平行四边形ABCD

=

1 2 AF

AD

=

1

4

．
过点作GH⊥AD，交AD于点G，交BC于点H，则EH⊥BC．
∵

AF

AD

=

1

2

，AD=BC，
∴

AF

BC

=

1

2

，
∴

GE

EH

=

1

2

，即GH=3GE．
∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC．
∴△AEF∽△CEB，
∴

S△AEF

S平行四边形ABCD

=

1 2 AF•GE

AD•GH

=

1 2 × 1 2 AD×GE

AD•3GE

=

1 4

3

=

1

12

．
故答案是：

1

4

，

1

12

．

点评：本题考查的是相似三角形的判定与性质，熟知相似三角形的对应边成比例是解答此题的关键．