题目内容
4.已知$\frac{x}{2}=\frac{y}{3}=\frac{z}{5}$,且3x+4z-2y=40,求x+y+z=20.分析 根据比例性质,可得3x=2y,可得关于y的方程,根据解方程,可得y的值,再根据比的意义,可得x、z的值,根据有理数的加法,可得答案.
解答 解:由$\frac{x}{2}$=$\frac{y}{3}$,得
3x=2y.
3x+4z-2y=40,
即4z=40,
解得z=10,
由$\frac{x}{2}=\frac{y}{3}=\frac{z}{5}$,得
$\frac{x}{2}=\frac{y}{3}=\frac{z}{5}$=$\frac{10}{5}$=2,
解得x=4,y=6,
x+y+z=4+6+10=20.
故答案为:20.
点评 本题考查了比例的性质,利用比例的性质得出3x=2y是解题关键,又利用比的意义得出x、y的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.一个直角三角形的两条直角边相差5cm,面积是7cm2,斜边长是( )
| A. | $\sqrt{14}$ | B. | $\sqrt{35}$ | C. | $\sqrt{53}$ | D. | $\sqrt{74}$ |
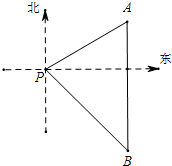 一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的东南方向上的B处.这时,海轮所在的B处距离灯塔P有多远?(结果保留根号)
一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的东南方向上的B处.这时,海轮所在的B处距离灯塔P有多远?(结果保留根号)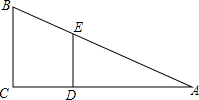 如图,上体育课,九年级三班的甲、乙两名同学分别站在C、D的位置时,乙的影子恰好在甲的影子里边,已知甲,乙同学相距1米.甲身高1.8米,乙身高1.5米,则甲的影长是( )
如图,上体育课,九年级三班的甲、乙两名同学分别站在C、D的位置时,乙的影子恰好在甲的影子里边,已知甲,乙同学相距1米.甲身高1.8米,乙身高1.5米,则甲的影长是( )