题目内容
13.△ABC中,AB=5,BC=8,∠ABC=60°,则△ABC的内切圆半径为$\sqrt{3}$.分析 作AD⊥BC于D,根据直角三角形的性质和勾股定理求出BD、AD的长,根据三角形的面积=$\frac{1}{2}$×(AB+BC+AC)×r计算即可.
解答 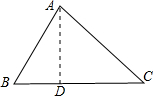 解:作AD⊥BC于D,
解:作AD⊥BC于D,
∵∠ABC=60°,
∴∠BAD=30°,∴BD=$\frac{1}{2}$AB=$\frac{5}{2}$,
∴AD=$\frac{5\sqrt{3}}{2}$,CD=BC-BD=$\frac{11}{2}$,
∴AC=7,
设△ABC的内切圆半径为r,
$\frac{1}{2}$×(AB+BC+AC)×r=$\frac{1}{2}$×BC×AD,
解得,r=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查的是三角形内心的性质,掌握三角形的内心是三角形三条角平分线的交点和角平分线的性质是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
8.如果将抛物线y=x2向右平移1个单位,再向上平移2个单位,那么所得的抛物线的表达式是( )
| A. | y=(x-1)2+2 | B. | y=(x-1)2-2 | C. | y=(x+1)2-2 | D. | y=(x+1)2+2 |
18.一个球的内部挖去一个最大的正方体(正方体的八个顶点都在球的表面上),用一个平面去截这个几何体,其截面形状有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.下列各组中的两个量,不是具有相反意义的是( )
| A. | 买进20棵树苗与种树10棵 | |
| B. | 一辆出租车向北行驶24米与向南行驶15米 | |
| C. | 盈利50元与亏损40元 | |
| D. | 气温升高3℃与气温降低5℃ |
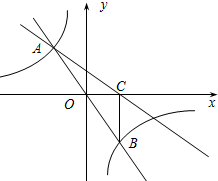 如图,在直角坐标系xOy中,直线y1=mx与双曲线y2=$\frac{n}{x}$相交于A(-1,a)、B两点,BC⊥x轴,垂足为C,△BOC的面积是1.
如图,在直角坐标系xOy中,直线y1=mx与双曲线y2=$\frac{n}{x}$相交于A(-1,a)、B两点,BC⊥x轴,垂足为C,△BOC的面积是1.