题目内容
15.求|x-1|+|x-2|+…+|x-2015|的最小值.分析 根据绝对值的性质,两端的数距原点越近,所求的绝对值越小,然后进行解答即可.
解答 解:∵2015=2×1008-1,
∴当x=1008时,|x-1|+|x-2|+…+|x-2015|有最小值.
∴当x=1008时,
|x-1|+|x-2|+…+|x-2015|
=1008-1+1008-2+1008-3+…+1008-1008+1009-1008+1010-1008+…+2015-1008
=2×(1+2+3+…+1007)
=1008×1007
=1015056.
点评 本题主要考查的是绝对值的性质、判定出当x=1008时,代数式有最小值是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
7. 如图,在平行四边形ABCD中,F是AD延长线上一点,连接BF交DC与点E,则图中相似三角形共有( )
如图,在平行四边形ABCD中,F是AD延长线上一点,连接BF交DC与点E,则图中相似三角形共有( )
 如图,在平行四边形ABCD中,F是AD延长线上一点,连接BF交DC与点E,则图中相似三角形共有( )
如图,在平行四边形ABCD中,F是AD延长线上一点,连接BF交DC与点E,则图中相似三角形共有( )| A. | 0对 | B. | 1对 | C. | 2对 | D. | 3对 |
4.x是一个两位数,y是一个不等于0的一位数,若把y放在x的左边,则新得的三位数是( )
| A. | yx | B. | y+x | C. | 10y+x | D. | 100y+x |
5.对于-1来说( )
| A. | 有平方根 | B. | 只有算术平方根 | C. | 没有平方根 | D. | 不能确定 |
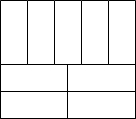 某居民小区为了绿化小区环境,建设和谐家园.准备将一块周长为76米的长方形空地,设计成长和宽分别相等的9块小长方形,如图所示.计划在空地上种上各种花卉,经市场预测,绿化每平方米空地造价110元,请计算,要完成这块绿化工程,预计花费多少元?
某居民小区为了绿化小区环境,建设和谐家园.准备将一块周长为76米的长方形空地,设计成长和宽分别相等的9块小长方形,如图所示.计划在空地上种上各种花卉,经市场预测,绿化每平方米空地造价110元,请计算,要完成这块绿化工程,预计花费多少元?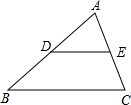 如图,在△ABC中,DE∥BC,△ADE的面积与梯形DBCE的面积相等,BC=4$\sqrt{2}$,那么DE的长度是?
如图,在△ABC中,DE∥BC,△ADE的面积与梯形DBCE的面积相等,BC=4$\sqrt{2}$,那么DE的长度是?