题目内容
20.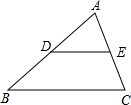 如图,在△ABC中,DE∥BC,△ADE的面积与梯形DBCE的面积相等,BC=4$\sqrt{2}$,那么DE的长度是?
如图,在△ABC中,DE∥BC,△ADE的面积与梯形DBCE的面积相等,BC=4$\sqrt{2}$,那么DE的长度是?
分析 首先根据题目中的三角形和四边形的面积求得三角形ADE和三角形ABC的面积的比,然后求得相似三角形的相似比,然后求得对应边的值即可.
解答 解:∵DE∥BC,
∴△ADE∽△ABC.
∵梯形DBCE面积与△ADE面积相等,
∴S△ADE:S△ABC=1:2,
∴$\frac{DE}{BC}$=$\sqrt{\frac{1}{2}}$=$\frac{\sqrt{2}}{2}$,
∵BC=4$\sqrt{2}$,
∴DE=4.
点评 本题考查的是相似三角形的判定与性质,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
5.命题:①“对顶角相等”的逆命题一定是真命题;②垂直于同一条直线的两直线平行;③如果一个三角形中有两边的平方和等于第三边的平方,那么这个三角形是直角三角形;④同位角相等.其中假命题有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.关于相似的下列说法正确的是( )
| A. | 所有直角三角形相似 | B. | 所有等腰三角形相似 | ||
| C. | 有一角是80°的等腰三角形相似 | D. | 所有等腰直角三角形相似 |
 如图,在一幅矩形地毯的四周镶有宽度相同的花边,如图,地毯中央的矩形图案长8米、宽6米,整个地毯的面积是120平方米,求花边的宽.
如图,在一幅矩形地毯的四周镶有宽度相同的花边,如图,地毯中央的矩形图案长8米、宽6米,整个地毯的面积是120平方米,求花边的宽.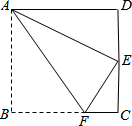 如图所示,四边形ABCD为长方形纸片,把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF,CD=6,求AF的长.
如图所示,四边形ABCD为长方形纸片,把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF,CD=6,求AF的长. 如图,已知DE∥BC,EF∥CD,且E在边AC上,F、D在边AB上,若AE:CE=2:1,DF=2,求AF、BD的长.
如图,已知DE∥BC,EF∥CD,且E在边AC上,F、D在边AB上,若AE:CE=2:1,DF=2,求AF、BD的长.