题目内容
20.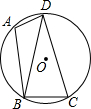 如图,己知四边形ABCD内接于圆O,连结BD,∠BAD=115°,∠DBC=65°.
如图,己知四边形ABCD内接于圆O,连结BD,∠BAD=115°,∠DBC=65°.(1)求证:BD=CD;
(2)若圆O的半径为6,求$\widehat{BC}$的长(结果保留π).
分析 (1)直接利用圆周角定理得出∠DCB的度数,再利用∠DCB=∠DBC求出答案;
(2)首先求出$\widehat{BC}$的度数,再利用弧长公式直接求出答案.
解答 (1)证明:∵四边形ABCD内接于圆O,
∴∠DCB+∠BAD=180°,
∵∠BAD=115°,
∴∠DCB=180°-115°=65°,
∵∠DBC=65°,
∴∠DCB=∠DBC=65°,
∴BD=CD;
(2)解:∵∠DCB=∠DBC=65°,
∴∠BDC=50°,
由圆周角定理,得$\widehat{BC}$的度数为:100°,
故$\widehat{BC}$=$\frac{nπr}{180}$=$\frac{100π×6}{180}$=$\frac{10}{3}$π,
答:$\widehat{BC}$的长为$\frac{10}{3}$π.
点评 此题主要考查了弧长公式应用以及圆周角定理等知识,根据题意得出∠DCB的度数是解题关键.

练习册系列答案
相关题目
10.△ABC中,∠A=25°,∠B=87°,则∠C=( )
| A. | 58° | B. | 68° | C. | 78° | D. | 87° |
11.下列四个方程中,是一元一次方程的是( )
| A. | 2x-y=1 | B. | x 2-3 x+1=0 | C. | x=7 | D. | $\frac{2}{x}$=1 |




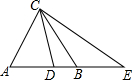 如图,△ABC中,AB=AC=8,D在AB上,E在AB的延长线上,∠ECB=∠DCB,AE=12.
如图,△ABC中,AB=AC=8,D在AB上,E在AB的延长线上,∠ECB=∠DCB,AE=12.