题目内容
3.用配方法解方程.x2+10x+16=0.分析 方程常数项移到右边,两边加上25变形后,开方即可求出解.
解答 解:方程变形得:x2+10x=-16,
配方得:x2+10x+25=-16+25,即(x+5)2=9,
开方得:x+5=±3,
解得:x1=-2,x2=-8.
点评 此题考查了解一元二次方程-配方法,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
13. 如图,菱形ABCD中,AC=16,BD=12,则菱形的周长是( )
如图,菱形ABCD中,AC=16,BD=12,则菱形的周长是( )
 如图,菱形ABCD中,AC=16,BD=12,则菱形的周长是( )
如图,菱形ABCD中,AC=16,BD=12,则菱形的周长是( )| A. | 20 | B. | 24 | C. | 28 | D. | 40 |
11.下列变形正确的是( )
| A. | $\sqrt{4\frac{9}{25}}$=$\sqrt{4}$×$\sqrt{\frac{9}{25}}$=2×$\sqrt{\frac{3}{5}}$=$\frac{6}{5}$ | B. | $\sqrt{4{1}^{2}-4{0}^{2}}$=$\sqrt{4{1}^{2}}$-$\sqrt{4{0}^{2}}$=41-40=1 | ||
| C. | 2$\sqrt{3}$×(-5$\sqrt{27}$)=-2×5×$\sqrt{3×27}$=-90 | D. | -3$\sqrt{2}$=$\sqrt{(-3)^{2}×2}$=$\sqrt{18}$ |
18.若n为正整数,则$\root{2n+1}{-1}$等于( )
| A. | -1 | B. | 1 | C. | ±1 | D. | 2n+1 |
12.设M=(4+2$\sqrt{3}$)3,其小数部分为P,则M(1-P)=( )
| A. | 58 | B. | 64 | C. | 73 | D. | 82 |
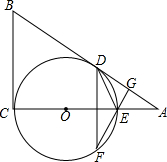 如图,已知AB和BC分别与圆O相切于点D、C,AC经过圆心O交圆于点E,AC=2AD且BD=2.
如图,已知AB和BC分别与圆O相切于点D、C,AC经过圆心O交圆于点E,AC=2AD且BD=2.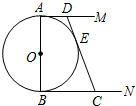 如图,⊙O的直径AB=2,AM和BN是它的两条切线,DE切⊙O于E,交AM于D,交BN 于C.设AD=x,BC=y.
如图,⊙O的直径AB=2,AM和BN是它的两条切线,DE切⊙O于E,交AM于D,交BN 于C.设AD=x,BC=y.