题目内容
16．
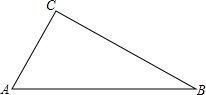如图，在△ABC中，∠C=90°．（1）试作出边AB的垂直平分线（要求：不写作法，保留作图痕迹）．
（2）若边AB的垂直平分线交BC于点E，连结AE，设CE=1，AC=2，则BE=$\sqrt{5}$．
分析 （1）利用线段垂直平分线的作法得出答案；
（2）利用线段垂直平分线的性质结合勾股定理得出AE的长，进而利用AE=BE得出答案．
解答 
解：（1）如图所示：MN即为所求；
（2）∵边AB的垂直平分线交BC于点E，
∴AE=BE，
∵CE=1，AC=2，∠C=90°，
∴AE=BE=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$．
故答案为：$\sqrt{5}$．
点评 此题主要考查了基本作图以及线段垂直平分线的性质与画法，正确掌握线段垂直平分线的性质是解题关键．
练习册系列答案
相关题目
6．方程2（1-x）=$\frac{1}{2}$x的解是（ ）
| A． | x=$\frac{4}{3}$ | B． | x=$\frac{4}{5}$ | C． | x=$\frac{2}{3}$ | D． | x=$\frac{5}{4}$ |
7．在$\sqrt{2}$，2，π，|-3|中，最大的数是（ ）
| A． | $\sqrt{2}$ | B． | 2 | C． | π | D． | |-3| |
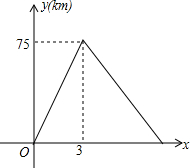在松花江沿岸依次有A、B、C旅游景点，一观光游船由A景点顺流出发经过B景点到达C景点后立即返回，A、B两个景点之间的距离为25km，当游船到达B景点时恰好由一艘橡皮艇从B景点漂流而下，游船离开A景点的距离y（km）与其行驶时间x（h）之间的函数关系如图所示．
8．
如图所示，将一个正方形纸条剪去一个宽为5cm的长条后，再从剩下的长方形纸条上剪去一个宽为3cm的长条，如果第一次剪下的长条面枳是第二次剪下的长条面积的2倍，若设原正方形纸条的边长为xcm．则可列方程（ ）
如图所示，将一个正方形纸条剪去一个宽为5cm的长条后，再从剩下的长方形纸条上剪去一个宽为3cm的长条，如果第一次剪下的长条面枳是第二次剪下的长条面积的2倍，若设原正方形纸条的边长为xcm．则可列方程（ ）| A． | 5x=2×3（x-5） | B． | 2×5x=3（x-5） | C． | 5（x-3）=2×3x | D． | 2×5（x-3）=3x |