题目内容
1.矩形的两条对角线的夹角为60°,对角线长为12,则较短的边长为6.分析 如下图所示:∠AOD=∠BOC=60°,即:∠COD=120°>∠AOD=60°,AD是该矩形较短的一边,根据矩形的性质:矩形的对角线相等且互相平分,所以有OA=OD=OC=OB=6,又因为∠AOD=∠BOC=60°,所以AD=OA=0D=6.
解答 解:如下图所示:矩形ABCD,对角线AC=BD=12,∠AOD=∠BOC=60°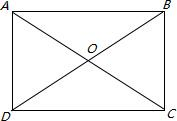 ∵四边形ABCD是矩形
∵四边形ABCD是矩形
∴OA=OD=OC=OB=$\frac{1}{2}$×12=6(矩形的对角线互相平分且相等)
又∵∠AOD=∠BOC=60°,
∴OA=OD=AD=6,
∵∠COD=120°>∠AOD=60°
∴AD<DC
所以该矩形较短的一边长为6,
故答案为:6.
点评 本题主要考查矩形的性质:矩形的对角线相等且互相平分,且矩形对角线相交所的角中“大角对大边,小角对小边”.

练习册系列答案
相关题目
6.如国所示,为几何体的平面展开图,则从左到右,其对应的几何体名称分别为( )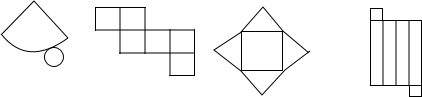

| A. | 圆锥,正方体,四棱锥,四梭柱 | B. | 圆柱,正方体,四棱锥,四梭柱 | ||
| C. | 圆锥,正方体,四棱柱,四梭锥 | D. | 圆柱,正方体,四棱柱,四梭锥 |
 已知∠α和线段a,求作△ABC,使∠A=∠α,∠B=$\frac{1}{2}$∠α,AB=a.
已知∠α和线段a,求作△ABC,使∠A=∠α,∠B=$\frac{1}{2}$∠α,AB=a. 如图,在△ABC中,∠C=90°.
如图,在△ABC中,∠C=90°.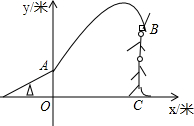 如图,杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线y=-$\frac{1}{3}$x2+2x+4的一部分.
如图,杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线y=-$\frac{1}{3}$x2+2x+4的一部分.