题目内容
 如图,等腰直角三角形ABC中,AD是底边BC上的高,现将△ABD沿DC方向平移,使点D和点C重合,若重叠部分(阴影部分)的面积是4,则△ABC的腰长为
如图,等腰直角三角形ABC中,AD是底边BC上的高,现将△ABD沿DC方向平移,使点D和点C重合,若重叠部分(阴影部分)的面积是4,则△ABC的腰长为考点:平移的性质
专题:
分析:根据等腰直角三角形的性质得出∠B=∠C=45°,故可得出△CDE是等腰直角三角形,根据重叠部分(阴影部分)的面积是4求出DE的长,故可得出CD的长,再根据勾股定理即可得出AC的长.
解答: 解:∵△ABC是等腰直角三角形,
解:∵△ABC是等腰直角三角形,
∴∠B=∠C=45°,
∴△CDE是等腰直角三角形.
∵重叠部分(阴影部分)的面积是4,
∴
DE2=4,解得DE=2
,
∴CD=
=
=4,
∴AC=
=
=4
.
故答案为:4
.
 解:∵△ABC是等腰直角三角形,
解:∵△ABC是等腰直角三角形,∴∠B=∠C=45°,
∴△CDE是等腰直角三角形.
∵重叠部分(阴影部分)的面积是4,
∴
| 1 |
| 2 |
| 2 |
∴CD=
| DE |
| sin45° |
2
| ||||
|
∴AC=
| 2CD2 |
| 2×42 |
| 2 |
故答案为:4
| 2 |
点评:本题考查的是平移的性质,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
 如图:AB⊥CD,CD为⊙O直径,且AB=20,CE=4,那么⊙O的半径是( )
如图:AB⊥CD,CD为⊙O直径,且AB=20,CE=4,那么⊙O的半径是( )A、
| ||
| B、14 | ||
C、
| ||
| D、15 |
以下四个说法中:①在同一直线上的4点A、B、C、D只能表示出5条不同的线段;②经过两点有一条直线,并且只有一条直线;③同一平面内过一点有且只有一条直线与已知直线垂直;④两条直线的位置关系只有相交和平行,说法都正确的结论是( )
| A、②③ | B、①④ |
| C、②③④ | D、①②③ |
 如图,AB是⊙O的直径,C、D是⊙O上两点,CD⊥AB,若∠DAB=65°,则∠AOC等于( )
如图,AB是⊙O的直径,C、D是⊙O上两点,CD⊥AB,若∠DAB=65°,则∠AOC等于( )| A、25° | B、30° |
| C、50° | D、65° |
 如图,A,B是小河同侧的两个村庄,为解决吃水问题,两村合资在河边修一个水站.
如图,A,B是小河同侧的两个村庄,为解决吃水问题,两村合资在河边修一个水站.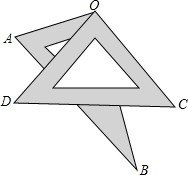 如图,将一副三角板叠放在一起,使直角顶点重合于O点,则∠AOC+∠BOD=
如图,将一副三角板叠放在一起,使直角顶点重合于O点,则∠AOC+∠BOD= 如图,是一个被分成6等份的扇形转盘,小明转了2次结果指针都停留在红色区域,小明第3次再转动指针停留在红色区域的概率是
如图,是一个被分成6等份的扇形转盘,小明转了2次结果指针都停留在红色区域,小明第3次再转动指针停留在红色区域的概率是