题目内容
12.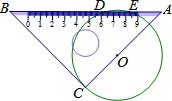 数学兴趣小组活动时,小明将一块等腰直角三角板(其中斜边上带有刻度)的直角顶点C放在⊙O上的任意一点,转动三角板,使其一条直角边AC经过圆心O,此时小明发现三角板的斜边AB在⊙O上截得的线段(DE)长为2厘米,已知三角板的直角边长为7厘米,则⊙O的半径为( )
数学兴趣小组活动时,小明将一块等腰直角三角板(其中斜边上带有刻度)的直角顶点C放在⊙O上的任意一点,转动三角板,使其一条直角边AC经过圆心O,此时小明发现三角板的斜边AB在⊙O上截得的线段(DE)长为2厘米,已知三角板的直角边长为7厘米,则⊙O的半径为( )| A. | 3厘米 | B. | $\frac{20}{7}$厘米 | C. | $\sqrt{10}$厘米 | D. | $2\sqrt{2}$厘米 |
分析 利用垂径定理得ME=DM=1,利用勾股定理和等腰三角形的性质得OM与DO的关系式,解得结果.
解答  解:过O点作OM⊥AB,
解:过O点作OM⊥AB,
∴ME=DM=1cm,
设MO=h,CO=DO=x,
∵△ABC为等腰直角三角形,AC=BC,
∴∠MAO=45°,
∴AO=$\sqrt{2}$h
∵AO=7-x,
∴$\sqrt{2}h=7-x$,
在Rt△DMO中,
h2=x2-1,
∴2x2-2=49-14x+x2,解得:x=-17(舍去)或x=3,
故选A
点评 本题主要考查了勾股定理,垂径定理,等腰三角形的性质,作出适当的辅助线,数形结合,建立等量关系是解答此题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
17. 如图,正方形ABCD中,点E,F分别在BC,CD上,△AEF是等边三角形,连接AC交EF于点G,下列结论:①CE=CF,②∠AEB=75°,③AG=2GC,④BE+DF=EF,⑤S△CEF=2S△ABE,其中结论正确的个数为( )
如图,正方形ABCD中,点E,F分别在BC,CD上,△AEF是等边三角形,连接AC交EF于点G,下列结论:①CE=CF,②∠AEB=75°,③AG=2GC,④BE+DF=EF,⑤S△CEF=2S△ABE,其中结论正确的个数为( )
 如图,正方形ABCD中,点E,F分别在BC,CD上,△AEF是等边三角形,连接AC交EF于点G,下列结论:①CE=CF,②∠AEB=75°,③AG=2GC,④BE+DF=EF,⑤S△CEF=2S△ABE,其中结论正确的个数为( )
如图,正方形ABCD中,点E,F分别在BC,CD上,△AEF是等边三角形,连接AC交EF于点G,下列结论:①CE=CF,②∠AEB=75°,③AG=2GC,④BE+DF=EF,⑤S△CEF=2S△ABE,其中结论正确的个数为( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
1.下列各数中,没有平方根的是( )
| A. | (-2)2 | B. | 64 | C. | $\frac{1}{2}$ | D. | -22 |
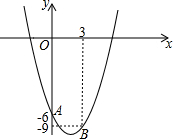 如图,已知抛物线y=ax2-4x+c经过点A(0,-6)和B(3,-9).
如图,已知抛物线y=ax2-4x+c经过点A(0,-6)和B(3,-9).