题目内容
4.解方程:(1)(x-3)2+2x(x-3)=0
(2)x2-3x+2=0
(3)x2-4x+1=0
(4)2x2-5x-3=0.
分析 (1)利用因式分解法解方程;
(2)利用因式分解法解方程;
(3)先利用配方法得到(x-2)2=3,然后利用直接开平方法解方程;
(4)利用因式分解法解方程.
解答 解:(1)(x-3)(x-3+2x)=0,
x-3=0或x-3+2x=0,
所以x1=3,x2=1;
(2)(x-2)(x-1)=0,
x-2=0或x-1=0,
所以x1=2,x2=1;
(3)x2-4x+4=3,
(x-2)2=3,
x-2=±$\sqrt{3}$,
所以x1=2+$\sqrt{3}$,x2=2-$\sqrt{3}$;
(4)(2x+1)(x-3)=0,
2x+1=0或x-3=0,
所以x1=-$\frac{1}{2}$,x2=3.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了配方法解一元二次方程.

练习册系列答案
相关题目
12.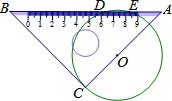 数学兴趣小组活动时,小明将一块等腰直角三角板(其中斜边上带有刻度)的直角顶点C放在⊙O上的任意一点,转动三角板,使其一条直角边AC经过圆心O,此时小明发现三角板的斜边AB在⊙O上截得的线段(DE)长为2厘米,已知三角板的直角边长为7厘米,则⊙O的半径为( )
数学兴趣小组活动时,小明将一块等腰直角三角板(其中斜边上带有刻度)的直角顶点C放在⊙O上的任意一点,转动三角板,使其一条直角边AC经过圆心O,此时小明发现三角板的斜边AB在⊙O上截得的线段(DE)长为2厘米,已知三角板的直角边长为7厘米,则⊙O的半径为( )
 数学兴趣小组活动时,小明将一块等腰直角三角板(其中斜边上带有刻度)的直角顶点C放在⊙O上的任意一点,转动三角板,使其一条直角边AC经过圆心O,此时小明发现三角板的斜边AB在⊙O上截得的线段(DE)长为2厘米,已知三角板的直角边长为7厘米,则⊙O的半径为( )
数学兴趣小组活动时,小明将一块等腰直角三角板(其中斜边上带有刻度)的直角顶点C放在⊙O上的任意一点,转动三角板,使其一条直角边AC经过圆心O,此时小明发现三角板的斜边AB在⊙O上截得的线段(DE)长为2厘米,已知三角板的直角边长为7厘米,则⊙O的半径为( )| A. | 3厘米 | B. | $\frac{20}{7}$厘米 | C. | $\sqrt{10}$厘米 | D. | $2\sqrt{2}$厘米 |

 如图,矩形ABCD的边长是常量,点E在AD上以每秒3个单位的速度从D运动到A,当运动时间为1秒时,△ABE的面积为10;当运动时间为2秒时,△ABE的面积为4.
如图,矩形ABCD的边长是常量,点E在AD上以每秒3个单位的速度从D运动到A,当运动时间为1秒时,△ABE的面积为10;当运动时间为2秒时,△ABE的面积为4.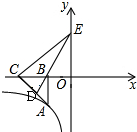 如图,已知点A在反比例函数y=$\frac{k}{x}$(x<0)上,作Rt△ABC,点D是斜边AC的中点,连DB并延长交y轴于点E,若△BCE的面积为8,则k的值为( )
如图,已知点A在反比例函数y=$\frac{k}{x}$(x<0)上,作Rt△ABC,点D是斜边AC的中点,连DB并延长交y轴于点E,若△BCE的面积为8,则k的值为( ) 在某公益活动中,小明对本年级同学的捐款情况进行了统计,绘制成如图所示的不完整的统计图,其中捐10元的人数占年级总人数的25%,则本次捐款20元的人数为35人.
在某公益活动中,小明对本年级同学的捐款情况进行了统计,绘制成如图所示的不完整的统计图,其中捐10元的人数占年级总人数的25%,则本次捐款20元的人数为35人.