题目内容
17. 如图,正方形ABCD中,点E,F分别在BC,CD上,△AEF是等边三角形,连接AC交EF于点G,下列结论:①CE=CF,②∠AEB=75°,③AG=2GC,④BE+DF=EF,⑤S△CEF=2S△ABE,其中结论正确的个数为( )
如图,正方形ABCD中,点E,F分别在BC,CD上,△AEF是等边三角形,连接AC交EF于点G,下列结论:①CE=CF,②∠AEB=75°,③AG=2GC,④BE+DF=EF,⑤S△CEF=2S△ABE,其中结论正确的个数为( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 通过条件可以得出△ABE≌△ADF,从而得出∠BAE=∠DAF,BE=DF,得到CE=CF;由正方形的性质就可以得出∠AEB=75°;设EC=x,由勾股定理得到EF,表示出BE,利用三角形的面积公式分别表示出S△CEF和2S△ABE,再通过比较大小就可以得出结论.
解答 解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=∠D=∠BAD=90°.
∵△AEF等边三角形,
∴AE=EF=AF,∠EAF=60°.
∴∠BAE+∠DAF=30°.
在Rt△ABE和Rt△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{AE=AF}\end{array}\right.$,
Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∴CE=CF,故①正确;
∵∠BAE=∠DAF,
∴∠DAF+∠DAF=30°,
即∠DAF=15°,
∴∠AEB=75°,故②正确;
设EC=x,由勾股定理,得
EF=$\sqrt{2}$x,CG=$\frac{\sqrt{2}}{2}$x,
AG=AEsin60°=EFsin60°=2×CGsin60°=$\frac{\sqrt{6}}{2}$x,
∴AG≠2GC,③错误;
∵CG=$\frac{\sqrt{2}}{2}$x,AG=$\frac{\sqrt{6}}{2}$x,
∴AC=$\frac{\sqrt{2}+\sqrt{6}}{2}$x
∴AB=AC•$\frac{\sqrt{2}}{2}$=$\frac{1+\sqrt{3}}{2}$x,
∴BE=$\frac{1+\sqrt{3}}{2}$x-x=$\frac{\sqrt{3}-1}{2}$x,
∴BE+DF=($\sqrt{3}$-1)x,
∴BE+DF≠EF,故④错误;
∵S△CEF=$\frac{1}{2}$x2,
S△ABE=$\frac{1}{2}$×BE×AB=$\frac{1}{2}×$$\frac{1+\sqrt{3}}{2}$x×$\frac{\sqrt{3}-1}{2}$x=$\frac{1}{4}$x2,
∴2S△ABE═S△CEF,故⑤正确.
综上所述,正确的有3个,
故选:B.
点评 本题考查了正方形的性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,等边三角形的性质的运用,三角形的面积公式的运用,解答本题时运用勾股定理的性质解题时关键.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案| A. | -2 | B. | $\frac{22}{7}$ | C. | $\sqrt{3}$ | D. | 0.101001000 |
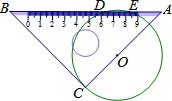 数学兴趣小组活动时,小明将一块等腰直角三角板(其中斜边上带有刻度)的直角顶点C放在⊙O上的任意一点,转动三角板,使其一条直角边AC经过圆心O,此时小明发现三角板的斜边AB在⊙O上截得的线段(DE)长为2厘米,已知三角板的直角边长为7厘米,则⊙O的半径为( )
数学兴趣小组活动时,小明将一块等腰直角三角板(其中斜边上带有刻度)的直角顶点C放在⊙O上的任意一点,转动三角板,使其一条直角边AC经过圆心O,此时小明发现三角板的斜边AB在⊙O上截得的线段(DE)长为2厘米,已知三角板的直角边长为7厘米,则⊙O的半径为( )| A. | 3厘米 | B. | $\frac{20}{7}$厘米 | C. | $\sqrt{10}$厘米 | D. | $2\sqrt{2}$厘米 |
| A. | 内含 | B. | 内切 | C. | 外切 | D. | 相交 |
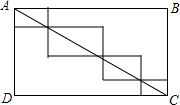 如图,长方形ABCD的边AB=7,BC=4,则图中四个小长方形的周长之和为22.
如图,长方形ABCD的边AB=7,BC=4,则图中四个小长方形的周长之和为22.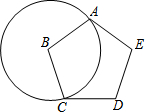 如图所示,正五边形ABCDE的边长为1,⊙B过五边形的顶点A、C,则劣弧AC的长为$\frac{3}{5}$π.
如图所示,正五边形ABCDE的边长为1,⊙B过五边形的顶点A、C,则劣弧AC的长为$\frac{3}{5}$π.