题目内容
 如图所示,在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,求作Rt△ABC的内切圆并求出△ABC内切圆的半径.
如图所示,在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,求作Rt△ABC的内切圆并求出△ABC内切圆的半径.考点:三角形的内切圆与内心,作图—复杂作图
专题:
分析:作∠A和∠B的角平分线,即可得出圆心O,再确定半径,即可得出⊙O,根据三角形的面积公式求出半径即可.
解答:解:如图:
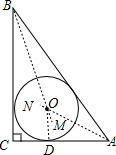
分别作∠A的平分线AM,∠B的平分线BN,AM和BN交于O,
过O作OD⊥AC于D,
以O为圆心,以OD为半径作圆,
则⊙O为所求;
如图,切点为D、E、F,连接OA、OB、OC,OE、OF,
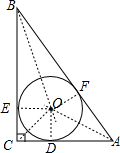
由勾股定理得:AB=
=5(cm),
设⊙O的半径是Rcm,则OD=OE=OF=Rcm,
∵S△ACB=S△BCO+S△ACO+S△ABO,
∴
×3×4=
×4R+
×3R+
×5R,
∴R=1cm,
△ABC内切圆的半径为1cm.

分别作∠A的平分线AM,∠B的平分线BN,AM和BN交于O,
过O作OD⊥AC于D,
以O为圆心,以OD为半径作圆,
则⊙O为所求;
如图,切点为D、E、F,连接OA、OB、OC,OE、OF,

由勾股定理得:AB=
| 32+42 |
设⊙O的半径是Rcm,则OD=OE=OF=Rcm,
∵S△ACB=S△BCO+S△ACO+S△ABO,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴R=1cm,
△ABC内切圆的半径为1cm.
点评:本题考查了勾股定理,三角形的内切圆与内心,三角形的面积的应用,主要考查了学生的动手操作能力能力和计算能力,题目比较好,难度适中.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
下列事件中,是必然事件的是( )
| A、抛掷一枚质地均匀的硬币,落地后正面朝上 | ||
| B、有一组临边相等的平行四边形是矩形 | ||
C、若a>0,则
| ||
| D、打开电视,正在播放节目《最强大脑》 |
 如图,为了检查墙壁上的木条AB与水平线CD是否平行,小华测得∠1=108°,∠2=72°,问直线AB与CD平行吗?为什么?
如图,为了检查墙壁上的木条AB与水平线CD是否平行,小华测得∠1=108°,∠2=72°,问直线AB与CD平行吗?为什么? 如图,在正方形ABCD,∠EAF=45°,交BC、CD于E、F,交BD于H、G,求证:BG•DH为定值.
如图,在正方形ABCD,∠EAF=45°,交BC、CD于E、F,交BD于H、G,求证:BG•DH为定值.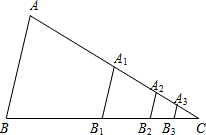 如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,则四边形A1ABB1的面积为
如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,则四边形A1ABB1的面积为 如图,扇形的弧长是20π,面积是240π,则此扇形的圆心角的度数是
如图,扇形的弧长是20π,面积是240π,则此扇形的圆心角的度数是