题目内容
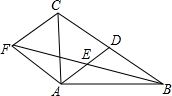 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.(1)求证:AF=DB;
(2)若AB⊥AC,试判断四边形AFCD的形状,并证明你的结论.
考点:全等三角形的判定与性质,菱形的判定
专题:
分析:(1)根据平行线的性质推出∠AFB=∠DBE,AAS证△AEF≌△DEB,根据全等三角形的性质推出即可;
(2)推出AF=CD,根据平行四边形的判定得出平行四边形,求出AD=CD,根据菱形的判定推出即可.
(2)推出AF=CD,根据平行四边形的判定得出平行四边形,求出AD=CD,根据菱形的判定推出即可.
解答:(1)证明:∵E是AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFB=∠DBE,
在△AEF和△DEB中
∴△AEF≌△DEB(AAS),
∴AF=BD;
(2)四边形AFCD是菱形,
证明:∵D为BC的中点,
∴CD=BD,
∵AF=BD,
∴AF=CD,
∵AF∥BC,
∴四边形AFCD是平行四边形,
∵AC⊥AB,
∴∠CAB=90°,
∵D为BC的中点,
∴AD=DC,
∴四边形AFCD是菱形.
∴AE=DE,
∵AF∥BC,
∴∠AFB=∠DBE,
在△AEF和△DEB中
|
∴△AEF≌△DEB(AAS),
∴AF=BD;
(2)四边形AFCD是菱形,
证明:∵D为BC的中点,
∴CD=BD,
∵AF=BD,
∴AF=CD,
∵AF∥BC,
∴四边形AFCD是平行四边形,
∵AC⊥AB,
∴∠CAB=90°,
∵D为BC的中点,
∴AD=DC,
∴四边形AFCD是菱形.
点评:本题考查了平行四边形的判定,菱形的判定,全等三角形的性质和判定的应用,主要考查学生的推理能力.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 如图,在△ABC中,点D、E分别是边AB,AC的中点,将△ADE绕点E旋转180°得△CFE,连结AF,CD,添加下列条件后能判定四边形ADCF是正方形的是( )
如图,在△ABC中,点D、E分别是边AB,AC的中点,将△ADE绕点E旋转180°得△CFE,连结AF,CD,添加下列条件后能判定四边形ADCF是正方形的是( )| A、AC=BC |
| B、∠ACB=90° |
| C、AC=BC且∠B=45° |
| D、AC=BC且∠B=60° |
 以边长为2的正方形的中心O为端点,引两条相互垂直的射线,分别与正方形的边交于A、B两点,则线段AB的最小值是多少?
以边长为2的正方形的中心O为端点,引两条相互垂直的射线,分别与正方形的边交于A、B两点,则线段AB的最小值是多少? 如图,平行四边形ABCD中,AC丄BC,E为AB的中点.若CE=2,求CD的长?
如图,平行四边形ABCD中,AC丄BC,E为AB的中点.若CE=2,求CD的长?