题目内容
1．已知△ABC∽△DEF，AB：DE=1：2，则△ABC与△DEF的周长比等于（ ）| A． | 1：2 | B． | 1：4 | C． | 2：1 | D． | 4：1 |
分析 直接根据相似三角形的性质即可得出结论．
解答 解：∵△ABC∽△DEF，AB：DE=1：2，
∴△ABC与△DEF的周长比=1：2．
故选A．
点评 本题考查的是相似三角形的性质，熟知相似三角形边长的比等于相似比，对应中线、对应角平分线、对应边上的高的比也等于相似比是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
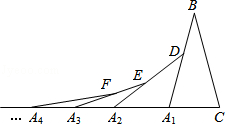如图，在第一个△A1BC中，∠B=30°，A1B=CB，在边A1B上任取一D，延长CA2到A2，使A1A2=A1D，得到第2个△A1A2D，在边A2B上任取一点E，延长A1A2到A3，使A2A3=A2E，得到第三个△A2A3E，…按此做法继续下去，第n个等腰三角形的底角的度数是$\frac{75}{{2}^{n-1}}$度．
12．若x=-1是关x的一元二次方程x2+a=0的一个根，则a的值为（ ）
| A． | -2 | B． | -1 | C． | 1 | D． | 2 |
10．下列说法中错误的是（ ）
| A． | 有理数可以分为正有理数、负有理数和零 | |
| B． | 0的相反数等于它本身 | |
| C． | 0既不是正数也不是负数 | |
| D． | 任何一个有理数的绝对值都是正数 |