题目内容
9.先化简.再求值:($\frac{x-1}{x}$-$\frac{x-2}{x+1}$)÷$\frac{2{x}^{2}-x}{{x}^{2}+2x+1}$,其中x满足x2-x-1=0.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到结果,将已知等式变形后代入计算即可求出值.
解答 解:原式=$\frac{{x}^{2}-1-{x}^{2}+2x}{x(x+1)}$•$\frac{(x+1)^{2}}{x(2x-1)}$
=$\frac{2x-1}{x(x+1)}$•$\frac{(x+1)^{2}}{x(2x-1)}$
=$\frac{x+1}{{x}^{2}}$,
∵x2-x-1=0,
∴x2=x+1,
∴原式=1.
点评 本题主要考查分式的化简求值,熟练掌握分式的基本性质和运算法则是解题的关键.

练习册系列答案
相关题目
20.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14.下列计算正确的是( )
| A. | (2x)3=2x3 | B. | (x+1)2=x2+1 | C. | (x2)3=x6 | D. | x2+x3=x5 |
1.已知△ABC∽△DEF,AB:DE=1:2,则△ABC与△DEF的周长比等于( )
| A. | 1:2 | B. | 1:4 | C. | 2:1 | D. | 4:1 |
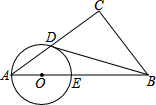 已知:如图所示,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A,求证:BD与⊙O相切.
已知:如图所示,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A,求证:BD与⊙O相切.