题目内容
 二次函数y=ax2+bx+c(a≠0)的图象大致如图所示,关于二次函数,下列说法错误的是( )
二次函数y=ax2+bx+c(a≠0)的图象大致如图所示,关于二次函数,下列说法错误的是( )| A、abc>0 | ||
B、对称轴是x=
| ||
C、当x<
| ||
| D、当-1<x<2时,y>0 |
考点:二次函数的图象,二次函数的性质
专题:数形结合
分析:由抛物线开口向上得a>0,由对称轴在y轴的右侧得b<0,由抛物线与y轴的交点在x轴下方得c<0,则有abc>0;根据抛物线的对称性可得到抛物线的对称轴为直线x=
;根据二次函数的性质可得当x<
时,y随x的增大而减小;观察函数图象得到当-1<x<2时,图象在x轴下方,则y<0.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵抛物线开口向上,
∴a>0,
∵对称轴在y轴的右侧,
∴b<0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc>0;
∵抛物线与x轴的交点坐标为(-1,0)、(2,0),
∴抛物线的对称轴为直线x=
;
∵抛物线开口向上,
∴当x<
时,y随x的增大而减小;
当-1<x<2时,y<0.
故选D.
∴a>0,
∵对称轴在y轴的右侧,
∴b<0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc>0;
∵抛物线与x轴的交点坐标为(-1,0)、(2,0),
∴抛物线的对称轴为直线x=
| 1 |
| 2 |
∵抛物线开口向上,
∴当x<
| 1 |
| 2 |
当-1<x<2时,y<0.
故选D.
点评:本题考查了二次函数的图象:y=ax2+bx+c的图象为抛物线,可利用列表、描点、连线画出二次函数的图象.也考查了二次函数的性质.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
下面的图形中是正方体的展开图的是( )
A、 |
B、 |
C、 |
D、 |
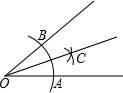 如图,用直尺和圆规作一个角的平分线,是运用了“全等三角形的对应角相等”这一性质,由作图所得条件,判定三角形全等运用的方法是( )
如图,用直尺和圆规作一个角的平分线,是运用了“全等三角形的对应角相等”这一性质,由作图所得条件,判定三角形全等运用的方法是( )| A、SAS | B、ASA |
| C、AAS | D、SSS |
 如图,在Rt△ABC和Rt△BAD中,CE=DE,∠C=∠D=90°.
如图,在Rt△ABC和Rt△BAD中,CE=DE,∠C=∠D=90°.