题目内容
20.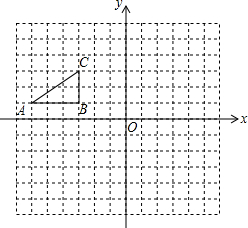 如图所示,方格纸中的每个小方格都是边长为1的正方形,Rt△ABC的项点均在格点上.A(-6,1)B(-3,1)C(-3,3)
如图所示,方格纸中的每个小方格都是边长为1的正方形,Rt△ABC的项点均在格点上.A(-6,1)B(-3,1)C(-3,3)(1)将Rt△ABC沿x轴正方向平移5个单位长度后得到Rt△A1B1C1.试在图中画出Rt△A1B1C1,并写出C1点的坐标;
(2)将Rt△ABC绕点B顺时针旋转90°后得到Rt△A2B2C2.试在图中画出Rt△A2B2C2.
分析 (1)把A、B、C的横坐标都加上5,纵坐标不变即可得到A1、B1、C1的坐标,然后描点即可得到RT△A1B1C1;
(2)利用网格特点和旋转的性质画出点A、B、C的对应点A2、B2、C2即可.
解答 解:(1)如图,RT△A1B1C1为所作,点C1的坐标为(2,3);
(2)如图,Rt△A2B2C2即为所作.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
10.下列各数中最小的数是( )
| A. | -2 | B. | -π | C. | -$\sqrt{3}$ | D. | 1 |
11.下列计算正确的是( )
| A. | (a2)3=a6 | B. | a2•a3=a6 | C. | (ab)2=ab2 | D. | a6÷a2=a3 |
12.不等式组$\left\{\begin{array}{l}x>0\\ x<1\end{array}\right.$的解集是( )
| A. | 0<x<1 | B. | x>0 | C. | x<1 | D. | 无解 |
9.把方程x2+4x+1=0配方成(x+p)2+q=0的形式后,p2+q2的值是( )
| A. | 41 | B. | 14 | C. | 13 | D. | 7 |
7.函数y=$\frac{\sqrt{x+2}}{x-1}$中,自变量x的取值范围是( )
| A. | x≥-2 | B. | x≥-2 且x≠1 | C. | x≠2 | D. | x≤-2 |
 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,-2),B(3,-1),C(1,-1).
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,-2),B(3,-1),C(1,-1).
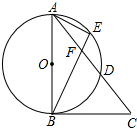 如图,在△ABC中,以AB为直径的⊙O与边AC交于点D,E为$\widehat{AD}$上的一点,BE交AC于点F,CF=BC,∠EAF=∠EBA.
如图,在△ABC中,以AB为直径的⊙O与边AC交于点D,E为$\widehat{AD}$上的一点,BE交AC于点F,CF=BC,∠EAF=∠EBA.