题目内容
19．已知|a-1|+|b-2|=0，则a100-5b=-24．分析 根据非负数的性质可求出a、b的值，再将它们代入求解即可．
解答 解：根据题意得：$\left\{\begin{array}{l}{a-1=0}\\{b-2=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$，
则a100-5b=1-52=1-25=-24．
故答案是：-24．
点评 本题考查了非负数的性质：有限个非负数的和为零，那么每一个加数也必为零．
练习册系列答案
相关题目
将一副直角三角尺如图叠放，若∠AOD=15°，则∠BOC=165°．
7．若-3xmy4与7x2yn-1是同类项，则m+n的值为（ ）
| A． | 5 | B． | 6 | C． | 7 | D． | 8 |
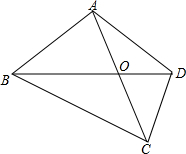如图所示，四边形ABCD中，对角线AC、BD交于点O，且AB=AD，AO=OC，请你猜想AB+BO与BC+OD的数量关系，并证明你的结论．
8．已知x，y为实数，且$\sqrt{x-1}$+3|y-2|=0，则x-y的值为（ ）
| A． | 3 | B． | -3 | C． | -1 | D． | 1 |
如图，在△ABC中，AD是△ABC的中线，tanB=$\frac{1}{2}$，cosC=$\frac{{\sqrt{2}}}{2}$，AC=2$\sqrt{2}$，求sin∠ADC的值．