题目内容
20．解不等式组：$\left\{\begin{array}{l}{x+3＞0}\\{2（x-1）+3≥3x}\end{array}\right.$，把解集在数轴上表示出来，并判断-1，3这两个数是否为该不等式组的解．分析 先求出不等式组中每一个不等式的解集，再求出它们的公共部分，然后把不等式的解集表示在数轴上即可．
解答 解：$\left\{\begin{array}{l}{x+3＞0…①}\\{2（x-1）+3≥3x…②}\end{array}\right.$，
解①得x＞-3，
解②得x≤1．
故不等式组的解集是-3＜x≤1．
-1是不等式的解，3不是不等式组的解．
点评 本题考查的是一元一次不等式组的解，解此类题目常常要结合数轴来判断．还可以观察不等式的解，若x＞较小的数、＜较大的数，那么解集为x介于两数之间．
练习册系列答案
相关题目
10．下列各式中是二元一次方程的是（ ）
| A． | x+3y=5 | B． | -xy-y=1 | C． | 2x-y+1 | D． | $\frac{x}{2}$+$\frac{7}{y}$=$\frac{1}{5}$ |
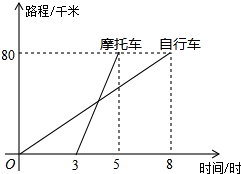如图表示一骑自行车者和一骑摩托车者沿相同的路线，由甲地到乙地行驶过程中路程和时间之间的关系图，已知两地相距80千米，请根据图象回答：
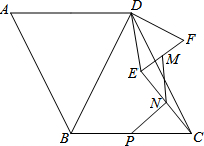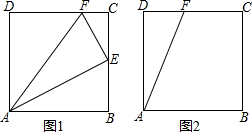
在?ABCD中，∠A=∠DBC，过点D作DE=DF，且∠EDF=∠ABD，连接EF、EC，M、N、P分别为EF、EC、BC的中点，连接NP．请你发现∠ABD与∠MNP满足的等量关系，并证明．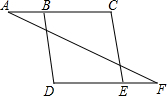
如图，已知∠A=∠F，∠C=∠D，试说明BD∥CE．