题目内容
15.如图,正方形ABCD边长为4,点E、F分别在边BC、CD上,且CF=1.(1)如图1,若E为BC的中点,请你证明△AEF是直角三角形;
(2)若E点在BC边内运动,当BE为多少时,(E为BC的中点),△AEF为直角三角形?
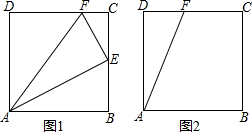
分析 (1)由正方形的性质得出∠B=∠C=∠D=90°,AB=BC=CD=4,由勾股定理及勾股定理的逆定理即可得出结论;
(2)证明△ABE∽△ECF,得出对应边成比例$\frac{BE}{CF}=\frac{AB}{CE}$,得出BE•CE=4,再由BE+CE=4即可得出结果.
解答 (1)证明:∵四边形ABCD是正方形,
∴∠B=∠C=∠D=90°,AB=BC=CD=4,
∵E为BC的中点,
∴BE=CE=2,
由勾股定理得:
AE2=AB2+BE2=42+22=20,
EF2=CE2+CF2=22+12=5,
AF2=AD2+DF2=42+32=25,
∴AE2+EF2=AF2,
∴△AEF是直角三角形;
(2)解:当BE=2时,△AEF为直角三角形;理由如下:
如图所示: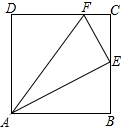 ∵∠AEF=90°,
∵∠AEF=90°,
∴∠AEB+∠CEF=90°,
∵∠BAE+∠AEB=90°,
∴∠BAE=∠CEF,
又∵∠B=∠C=90°,
∴△ABE∽△ECF,
∴$\frac{BE}{CF}=\frac{AB}{CE}$,
即$\frac{BE}{1}=\frac{4}{CE}$,
∴BE•CE=4,
又∵BE+CE=4,
∴BE=CE=2,
即当BE=2时,△AEF为直角三角形.
点评 本题考查了正方形的性质、勾股定理、勾股定理的逆定理、相似三角形的判定与性质;熟练掌握正方形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 四边形ABCD中,AB=CD,M、N是分别AD、BC的中点,延长BA、MN、CD分别交于点F、E,试说明∠1=∠2.
四边形ABCD中,AB=CD,M、N是分别AD、BC的中点,延长BA、MN、CD分别交于点F、E,试说明∠1=∠2.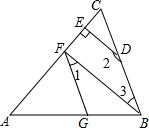 已知:如图,∠AGF=∠ABC,∠1+∠2=180°,DE⊥AC于点E.
已知:如图,∠AGF=∠ABC,∠1+∠2=180°,DE⊥AC于点E.