题目内容
12.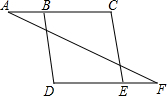 如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.
如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.证明:∵∠A=∠F (已知)
∴AC∥DF
∴∠+∠=180°两直线平行,同旁内角互补
∵∠C=∠D (已知)
∴∠D+∠DEC=180°
∴BD∥CE.
分析 由∠A=∠F,根据内错角相等,得两条直线平行,即AC∥DF;根据平行线的性质,得∠C=∠CEF,借助等量代换可以证明∠D=∠CEF,从而根据同位角相等,证明BD∥CE.
解答 证明:∵∠A=∠F (已知)
∴AC∥DF,
∴∠C+∠CED=180°(两直线平行,同旁内角互补)
∵∠C=∠D (已知)
∴∠D+∠DEC=180°
∴BD∥CE.
故答案为:AC,DF,两直线平行,同旁内角互补,BD∥CE.
点评 本题考查了平行线的判定与性质:同位角相等,两直线平行;同旁内角互补,两直线平行;内错角相等,两直线平行;两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
2.在x3-4x2+5x-k中,有一个因式为(x+2),则k的值为( )
| A. | -34 | B. | 34 | C. | 2 | D. | -2 |
 四边形ABCD中,AB=CD,M、N是分别AD、BC的中点,延长BA、MN、CD分别交于点F、E,试说明∠1=∠2.
四边形ABCD中,AB=CD,M、N是分别AD、BC的中点,延长BA、MN、CD分别交于点F、E,试说明∠1=∠2.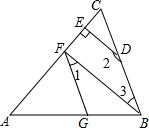 已知:如图,∠AGF=∠ABC,∠1+∠2=180°,DE⊥AC于点E.
已知:如图,∠AGF=∠ABC,∠1+∠2=180°,DE⊥AC于点E.