题目内容
2.有一矩形纸片ABCD,其中AB=2,以AD为直径的半圆正好与对边BC相切,将矩形纸片ABCD沿DE折叠,使点A落在BC上,如图2,则半圆露在外面的部分(阴影部分)的面积为$\frac{4}{3}$π-$\sqrt{3}$.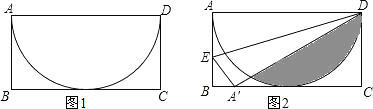
分析 如图,露在外面部分的面积可用扇形ODK与△ODK的面积差来求得,在Rt△A′DC中,可根据AD即圆的直径和CD即圆的半径长,求出∠DA′C的度数,进而得出∠ODH和∠DOK的度数,即可求得△ODK和扇形ODK的面积,由此可求得阴影部分的面积.
解答 解:作OH⊥DK于H,连接OK,
∵AB=2,
∴AD=A′D=4,CD=2,
∵以AD为直径的半圆,正好与对边BC相切,
∴AD=2CD,
∴A'D=2CD,
∵∠C=90°,
∴∠DA'C=30°,
∴∠ODH=30°,
∴∠DOH=60°,
∴∠DOK=120°,
∴扇形ODK的面积为$\frac{120π×{2}^{2}}{360}$=$\frac{4}{3}$π,
∵∠ODH=∠OKH=30°,OD=2,
∴OH=1,DH=$\sqrt{3}$cm;
∴DK=2$\sqrt{3}$cm,
∴△ODK的面积为$\sqrt{3}$,
∴半圆还露在外面的部分(阴影部分)的面积是:$\frac{4}{3}$π-$\sqrt{3}$.
故答案为:$\frac{4}{3}$π-$\sqrt{3}$.
点评 此题考查了折叠问题,圆的切线的性质,矩形的性质,掌握直角三角形中,如果有一条直角边是斜边的一半,那么这条直角边所对的角是30度是解决问题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
12.某商品经过连续两次降价,销售单价由原来的125元降到80元.设平均每次降价的百分率为x,由题意列方程:( )
| A. | 125(1-x)2=80 | B. | 125(1-2x)=80 | C. | 125(1-2x)2=80 | D. | 80(1-x)2=125 |
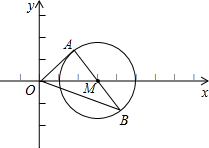 如图,平面直角坐标系xOy中,M点的坐标为(3,0),⊙M的半径为2,过M点的直线与⊙M的交点分别为A、B,则△AOB的面积的最大值为6.
如图,平面直角坐标系xOy中,M点的坐标为(3,0),⊙M的半径为2,过M点的直线与⊙M的交点分别为A、B,则△AOB的面积的最大值为6. 如图,CF⊥AB于点F,BE⊥AC于点E,且CF,BE交于点D,BD=CD.求证:AD平分∠BAC.
如图,CF⊥AB于点F,BE⊥AC于点E,且CF,BE交于点D,BD=CD.求证:AD平分∠BAC. 扇形AOB中,∠AOB=150°,AC=AO=6,D为AC的中点,当弦AC沿扇形运动时,点D所经过的路程为$\frac{3\sqrt{3}π}{2}$.
扇形AOB中,∠AOB=150°,AC=AO=6,D为AC的中点,当弦AC沿扇形运动时,点D所经过的路程为$\frac{3\sqrt{3}π}{2}$. 已知:如图,AE平分∠BAC,∠BAC=2∠B,AB=2AC.求证:(1)∠C=90°;(2)AE=2CE.
已知:如图,AE平分∠BAC,∠BAC=2∠B,AB=2AC.求证:(1)∠C=90°;(2)AE=2CE.