题目内容
14.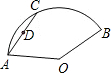 扇形AOB中,∠AOB=150°,AC=AO=6,D为AC的中点,当弦AC沿扇形运动时,点D所经过的路程为$\frac{3\sqrt{3}π}{2}$.
扇形AOB中,∠AOB=150°,AC=AO=6,D为AC的中点,当弦AC沿扇形运动时,点D所经过的路程为$\frac{3\sqrt{3}π}{2}$.
分析 由垂径定理求得线段OD的长也就是点D所经过圆弧路径的半径,然后求得路径的圆心角,利用弧长的计算公式计算即可.
解答 解:∵D为AC的中点,AC=AO=6,
∴OD⊥AC,
∴AD=$\frac{1}{2}$AO,
∴∠AOD=30°,OD=3$\sqrt{3}$,
同理可得:∠BOE=30°,
∴∠DOE=150°-60°=90°
∴点D所经过路径长为:$\frac{nπr}{180}=\frac{90π×3\sqrt{3}}{180}=\frac{3\sqrt{3}}{2}π$.
故答案为:$\frac{3\sqrt{3}π}{2}$
点评 本题考查了垂径定理、解直角三角形、弧长的计算等知识,解决本题的关键是根据题意确定点运动的路径是什么.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
5.根据天气预报显示,某市2012年元月1日的最高气温是6℃,最低气温是-4℃,那么,该市在这一天的最大温差为( )
| A. | 10℃ | B. | 6℃ | C. | 4℃ | D. | 2℃ |
4.等腰三角形的底和腰分别是方程x2-7x+10=0的两个根,则这个三角形的周长为( )
| A. | 9 | B. | 12 | C. | 9或12 | D. | 15 |

 已知:如图,AB⊥BC,AE⊥ED,垂足分别为点B,E,AB=AE,∠1=∠2,求证:BC=DE.
已知:如图,AB⊥BC,AE⊥ED,垂足分别为点B,E,AB=AE,∠1=∠2,求证:BC=DE.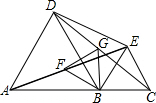 A,B,C在一条直线上,△ABD与△BCE为等边三角形,连AE,CD,F为AE的中点,G为CD的中点,判断△BFG的形状.
A,B,C在一条直线上,△ABD与△BCE为等边三角形,连AE,CD,F为AE的中点,G为CD的中点,判断△BFG的形状.