题目内容
12．已知关于x的一元二次方程（m+$\sqrt{3}$）${x}^{{m}^{2}-1}$+2（m-1）x-1=0，则m=$\sqrt{3}$．分析 根据一元二次方程的定义即可得出关于m的一元一次不等式及一元二次方程，解之即可得出结论．
解答 解：∵方程（m+$\sqrt{3}$）${x}^{{m}^{2}-1}$+2（m-1）x-1=0为一元二次方程，
∴$\left\{\begin{array}{l}{m+\sqrt{3}≠0}\\{{m}^{2}-1=2}\end{array}\right.$，
解得：m=$\sqrt{3}$．
故答案为：$\sqrt{3}$．
点评 本题考查了一元二次方程的定义，熟练掌握一元二次方程的定义是解题的关键．
练习册系列答案
相关题目
7．
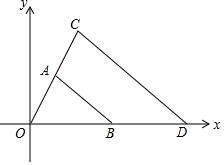如图，△AOB和△COD是以点O为位似中心的位似图形，点A的坐标为（1，2），点B的坐标为（3，0），相似比为1：2，则点C的坐标为（ ）
如图，△AOB和△COD是以点O为位似中心的位似图形，点A的坐标为（1，2），点B的坐标为（3，0），相似比为1：2，则点C的坐标为（ ）| A． | （2，3） | B． | （2，4） | C． | （3，3） | D． | （3，4） |
20．下面能判断两个三角形全等的条件是（ ）
| A． | 有两边及其中一边所对的角对应相等 | |
| B． | 三个角对应相等 | |
| C． | 两边和它们的夹角对应相等 | |
| D． | 两个三角形周长相等 |