题目内容
10．关于x的一元二次方程x2+（2m+1）x+m2-1=0有两个不相等的实数根，则m的取值范围是（ ）| A． | m≥-$\frac{5}{4}$ | B． | m≤-$\frac{5}{4}$ | C． | m＜-$\frac{5}{4}$ | D． | m＞-$\frac{5}{4}$ |
分析 根据方程的系数结合根的判别式即可得出关于m的一元一次不等式，解之即可得出结论．
解答 解：∵方程x2+（2m+1）x+m2-1=0有两个不相等的实数根，
∴△=（2m+1）2-4（m2-1）=4m+5＞0，
解得：m＞-$\frac{5}{4}$．
故选D．
点评 本题考查了根的判别式以及解一元一次不等式，熟练掌握“当△＞0时，方程有两个不相等的两个实数根”是解题的关键．
练习册系列答案
相关题目
20．在一个不透明的布袋中，红色、黑色、白色的玻璃球共有60个，除颜色外其它完全相同，小明通过多次摸球试验后发现其中摸到红色，黑色球的概率稳定在15%和40%，则口袋中白色球的个数很可能是（ ）
| A． | 25 | B． | 26 | C． | 29 | D． | 27 |
18．已知圆的半径为R，这个圆的内接正六边形的面积为（ ）
| A． | $\frac{3\sqrt{3}}{4}$R2 | B． | $\frac{3\sqrt{3}}{2}$R2 | C． | 6R2 | D． | 1.5R2 |
5．
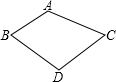如图，四边形ABCD，∠A=110°，若点D在AB、AC的垂直平分线上，则∠BDC为（ ）
如图，四边形ABCD，∠A=110°，若点D在AB、AC的垂直平分线上，则∠BDC为（ ）| A． | 90° | B． | 110° | C． | 120° | D． | 140° |
15．
如图，点B、C的坐标分别是（2，m），（8，4m-1），那么点A的坐标是（ ）
如图，点B、C的坐标分别是（2，m），（8，4m-1），那么点A的坐标是（ ）| A． | （-3，-2） | B． | （-2，-1） | C． | （-1，-2） | D． | （-4，-2） |
如图，直角三角形ABC以1cm/s的速度沿直线l向正方形DEFG移动，直到AB与DC重合时停止，移动前如图①所示，∠B=90°，AB=8cm，BC=6cm，正方形的边长为8cm．设移动x（s）时，三角形与正方形重叠部分的面积y（m2）
如图，一艘军舰位于点A处，在其正南方向有一目标B，在点B的正东方向有一目标C，且AB+BC=3海里，在AC上有一艘补给船D，DC为1海里；军舰从点A出发，向AB，BC方向匀速航行，补给船同时从点D出发，沿垂直于AC方向匀速直线航行，欲将一批物品送达军舰，已知军舰的速度是补给船的2倍，军舰在由B到C的途中与补给船相遇于E处，那么相遇时补给船航行了几海里？