题目内容
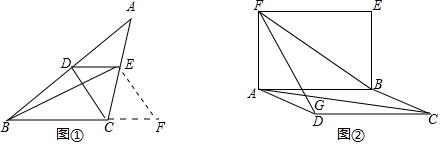
9.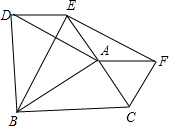 如图,?ADEF两边AD、AF向外作等边△ADB、△AFC,连接EB、EC、BC.
如图,?ADEF两边AD、AF向外作等边△ADB、△AFC,连接EB、EC、BC.(1)求证:△BDE≌△EFC;
(2)猜想:△EBC是等边三角形三角形,并对你的猜想加以证明.
分析 (1)根据SAS即可证明.
(2)由DE∥AF,推出∠6+∠4+∠1+∠8=180°,在△BDE中,根据内角和定理可知:∠5+∠3+∠2+∠8=180°,只要证明∠6=∠5,∠4=∠3,即可推出∠1=∠2=60°,由此即可证明.
解答 (1)证明:∵△ADB、△AFC都是等边三角形,
∴BD=AD,∠2=∠7=60°,CF=AF,
∵四边形DEFA是平行四边形,
∴AD=EF,AF=DE,∠5=∠6,
∴∠2+∠5=∠6+∠7,即∠BDE=∠EFC,
∴BD=EF,DE=FC,
在△EDB和△CFE中,
$\left\{\begin{array}{l}{ED=CF}\\{∠EDB=∠EFC}\\{DB=FE}\end{array}\right.$,
∴△BDE≌△EFC.
(2)解:∵△BDE≌△EFC,
∴BE=EC,∠3=∠4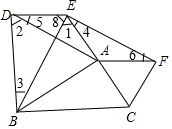 ,
,
∵DE∥AF,
∴∠6+∠4+∠1+∠8=180°,
在△BDE中,根据内角和定理可知:∠5+∠3+∠2+∠8=180°,
∵∠6=∠5,∠4=∠3,
∴∠1=∠2=60°,∵BE=EC,
∴△EBC是等边三角形.
点评 本题考查平行四边形的性质、等边三角形的性质、全等三角形的判定和性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有60个,除颜色外其它完全相同,小明通过多次摸球试验后发现其中摸到红色,黑色球的概率稳定在15%和40%,则口袋中白色球的个数很可能是( )
| A. | 25 | B. | 26 | C. | 29 | D. | 27 |
18.已知圆的半径为R,这个圆的内接正六边形的面积为( )
| A. | $\frac{3\sqrt{3}}{4}$R2 | B. | $\frac{3\sqrt{3}}{2}$R2 | C. | 6R2 | D. | 1.5R2 |
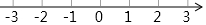 解不等式组$\left\{\begin{array}{l}{3x+1>-2}\\{\frac{x}{2}≥x-1}\end{array}\right.$,并将其解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{3x+1>-2}\\{\frac{x}{2}≥x-1}\end{array}\right.$,并将其解集在数轴上表示出来.