题目内容
13.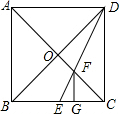 如图,在正方形ABCD中,对角线AC与BD相交于点O,点E是BC上的一个动点,连接DE,交AC于点F.
如图,在正方形ABCD中,对角线AC与BD相交于点O,点E是BC上的一个动点,连接DE,交AC于点F.(1)当$\frac{CE}{EB}$=$\frac{2}{3}$时,求$\frac{{S}_{△CEF}}{{S}_{△CDF}}$的值;
(2)当DE平分∠CDB时,求证:AF=$\sqrt{2}$OA;
(3)当点E是BC的中点时,过点F作FG⊥BC于点G,求证:CG=$\frac{1}{2}$BG.
分析 (1)利用相似三角形的性质求得EF与DF的比值,依据△CEF和△CDF同高,则面积的比就是EF与DF的比值,据此即可求解;
(2)利用三角形的外角和定理证得∠ADF=∠AFD,可以证得AD=AF,在直角△AOD中,利用勾股定理可以证得;
(3)连接OE,易证OE是△BCD的中位线,然后根据△FGC是等腰直角三角形,易证△EGF∽△ECD,利用相似三角形的对应边的比相等即可.
解答 解:(1)∵$\frac{CE}{EB}$=$\frac{2}{3}$,
∴$\frac{CE}{CB}$=$\frac{2}{5}$,
∵四边形ABCD是正方形,
∴AD∥BC,AD=BC,
∴△CEF∽△ADF,
∴$\frac{EF}{FD}$=$\frac{CE}{CB}$=$\frac{2}{5}$,
∴$\frac{{S}_{△CEF}}{{S}_{△CDF}}$=$\frac{2}{5}$;
(2)证明:∵DE平分∠CDB,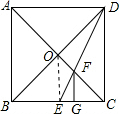
∴∠ODF=∠CDF,
∵AC、BD是正方形ABCD的对角线.
∴∠ADO=∠FCD=45°,∠AOD=90°,OA=OD,
而∠ADF=∠ADO+∠ODF,∠AFD=∠FCD+∠CDF,
∴∠ADF=∠AFD,
∴AD=AF,
在直角△AOD中,根据勾股定理得:AD=$\sqrt{O{A}^{2}+O{D}^{2}}$=$\sqrt{2}$OA,
∴AF=$\sqrt{2}$OA;
(3)证明:连接OE.
∵点O是正方形ABCD的对角线AC、BD的交点,
点O是BD的中点.
又∵点E是BC的中点,
∴OE是△BCD的中位线,
∴OE∥CD,OE=$\frac{1}{2}$CD,
∴△OFE∽△CFD,
∴$\frac{EF}{DF}$=$\frac{OE}{CD}$=$\frac{1}{2}$,
∵FG⊥BC,CD⊥BC,
∴FG∥CD,
∴△EGF∽△ECD,
∴$\frac{EG}{GC}$=$\frac{1}{2}$,
∵点E是BC的中点,
∴$\frac{CG}{GB}$=$\frac{1}{2}$,即CG=$\frac{1}{2}$BG.
点评 本题是正方形的性质、勾股定理、三角形的中位线定理、以及相似三角形的判定与性质的综合应用,正确理解相关的性质定理和判定定理是解题的关键.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案| A. | $\frac{3\sqrt{3}}{4}$R2 | B. | $\frac{3\sqrt{3}}{2}$R2 | C. | 6R2 | D. | 1.5R2 |
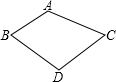 如图,四边形ABCD,∠A=110°,若点D在AB、AC的垂直平分线上,则∠BDC为( )
如图,四边形ABCD,∠A=110°,若点D在AB、AC的垂直平分线上,则∠BDC为( )| A. | 90° | B. | 110° | C. | 120° | D. | 140° |
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
 如图,AD∥BE,∠EDC=∠C,∠A与∠E相等吗?并说明理由.
如图,AD∥BE,∠EDC=∠C,∠A与∠E相等吗?并说明理由.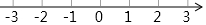 解不等式组$\left\{\begin{array}{l}{3x+1>-2}\\{\frac{x}{2}≥x-1}\end{array}\right.$,并将其解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{3x+1>-2}\\{\frac{x}{2}≥x-1}\end{array}\right.$,并将其解集在数轴上表示出来.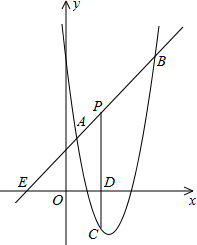 如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C. 如图,直角三角形ABC以1cm/s的速度沿直线l向正方形DEFG移动,直到AB与DC重合时停止,移动前如图①所示,∠B=90°,AB=8cm,BC=6cm,正方形的边长为8cm.设移动x(s)时,三角形与正方形重叠部分的面积y(m2)
如图,直角三角形ABC以1cm/s的速度沿直线l向正方形DEFG移动,直到AB与DC重合时停止,移动前如图①所示,∠B=90°,AB=8cm,BC=6cm,正方形的边长为8cm.设移动x(s)时,三角形与正方形重叠部分的面积y(m2)